Problem 1

Problem代写 Time variable being measured is the survival time in months. There are censored observations because there are patients alive
1.Time variable being measured is the survival time in months.
There are censored observations because there are patients alive at the date of the last contact (December 7, 2011). They are interval-censored because we don’t know exactly when the patients were dead but we know it was within some interval between the last patient follow-up and this follow-up.
2.In a ‘retrospective’ study, the result of interest (death) has already occurred at the start of the study.
3.In part A, Problem代写
the author presents study background which include study time range, patient backgrounds, location, study ethical stats, tumor size measurement standard and method. Also, the author presents descriptive statistics of tumor size and how to determine an optimal tumor size threshold. Then, the author presents group information and variables included in clinic-pathologic features.
In part B, the author presents mainly technical methodology used in survival analysis, which include time variable and cut-off date, how to test association between categorical variables, survival data estimation method, how to test difference in survival rates for subgroups of different tumor size, how to carry out multivariate analysis (Cos stepwise proportional hazard test), stratified univariate analysis and stratified multivariate analysis, criterion for statistical significance (p<0.05) and the data analysis tool (SPSS).
Part A and part B are different in the sense that part A concentrate more on the background and/or the preparation of the study and part B focus more on the carry-out and/or the progress of the survival analysis.
4.Thresholds of 4 cm. The null hypothesis is that there is no difference in survival between the patients whose tumor size is no larger than 4 cm and the patients whose tumor size is larger than 4 cm. The alternative hypothesis is that there is difference in survival between the patients whose tumor size is no larger than 4 cm and the patients whose tumor size is larger than 4 cm.
Thresholds of 5 cm. Problem代写
The null hypothesis is that there is no difference in survival between the patients whose tumor size is no larger than 5 cm and the patients whose tumor size is larger than 5 cm. The alternative hypothesis is that there is difference in survival between the patients whose tumor size is no larger than 5 cm and the patients whose tumor size is larger than 5 cm.
Thresholds of 6 cm. The null hypothesis is that there is no difference in survival between the patients whose tumor size is no larger than 6 cm and the patients whose tumor size is larger than 6 cm. The alternative hypothesis is that there is difference in survival between the patients whose tumor size is no larger than 6 cm and the patients whose tumor size is larger than 6 cm.
The threshold variable is measured according to the Japanese Classification of Gastric Cancer and the dissected stomach specimen was fixed on a flat board and the maximum tumor diameter was determined.
5.The threshold is defined when the chi-square value is maximized under log-rank test and Cox stepwise proportional hazard because it is mostly possible to observe group difference under a bigger chi-square value.
6.The curves are only for patients who underwent curative gastrectomy.
7.a)The curves are only for patients who underwent curative gastrectomy.
b)
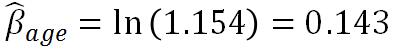
c) The variable is treated as continuous variable because the hazard ratio is calculated.
8.a) This is a stratified analysis without interaction because there are no variables in interaction form.
b) Tumor size is an independent prognostic factor in patients with stage T2, T3, T4 (but not for patients with stage T1) and the hazard ratio of tumor size decreases as the stage T grows.
In other words, for patients with stage T2, T3, T4, the death hazard is smaller for patients with advanced stages given the same tumor size. In addition, for patients with stage T1, only lymph node metastasis is an independent prognostic factor that impacting survival rate; tumor size is not statistically significant. For patients with stage T2 and T3, besides tumor size, lymph node metastasis, curability and age also significantly impact survival rate. For patients with stage 4, besides tumor size, lymph node metastasis and curability significantly impact survival rate.
9.Multivariate analysis (Table S3) and stage-stratified multivariate Cox stepwise proportional analysis (Figure 4, Figure 5, Figure 6, Figure 7).
Problem 2
b)
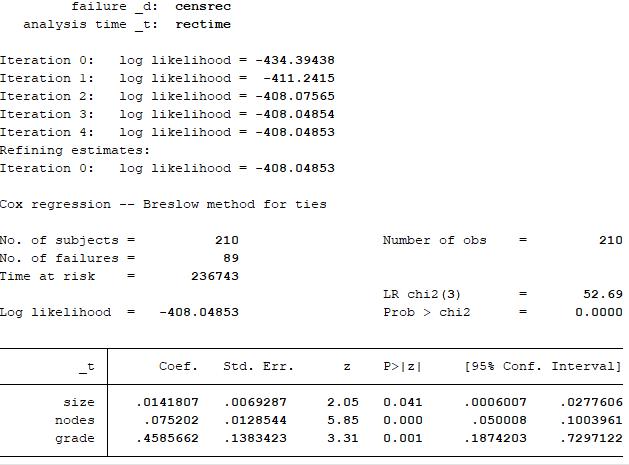
c)
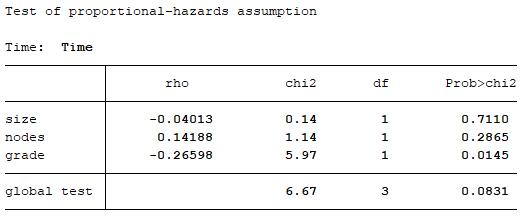
The result of statistical test shows that the p-value of ‘grade’ is 0.0145, indicating that the proportional-hazards assumption is violated at a 5% significance level. The result of statistical test shows that the p-value of ‘size’ and ‘nodes’ is 0.7110 and 0.2865, indicating that the proportional-hazard assumption is not violated even at a 10% significance level.
d)
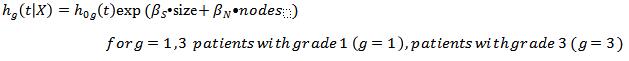
e)
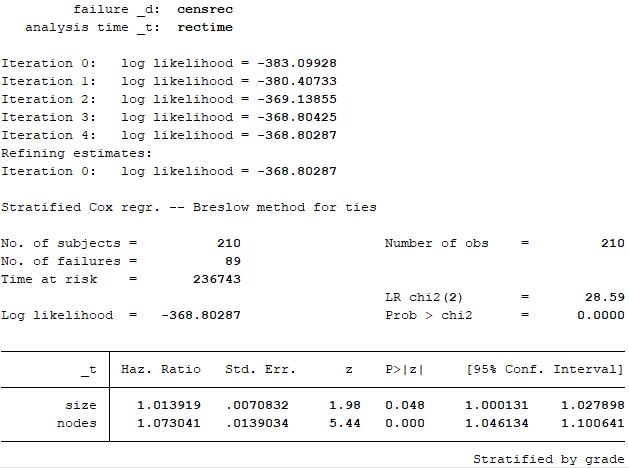
The drawback is that we cannot calculate hazard ratios form the stratifying variable, grade.Problem代写
f)
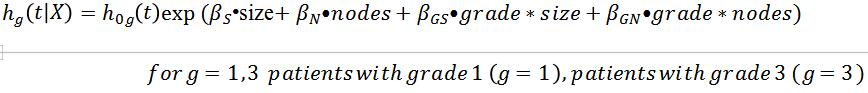
g)
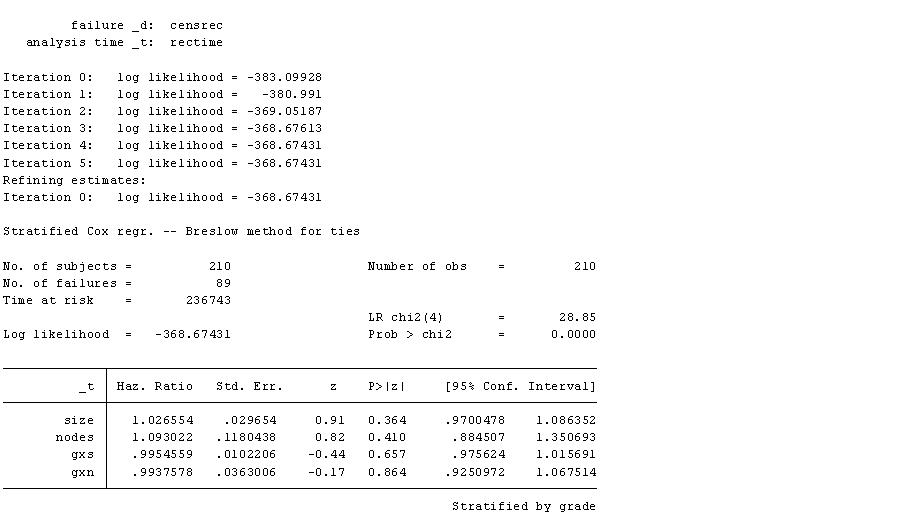
h)

The likelihood ratio test statistic is not significant, suggesting that the interaction terms are non-significant or that the no-interaction model is propriate.
i)
For the no-interaction model, the hazard ratio of nodes is 1.07, indicating that controlling for tumor size, the hazard of cancer recurrence is 1.07 times higher for patients with each additional increase of nodes.
Problem 3 Problem代写
a.
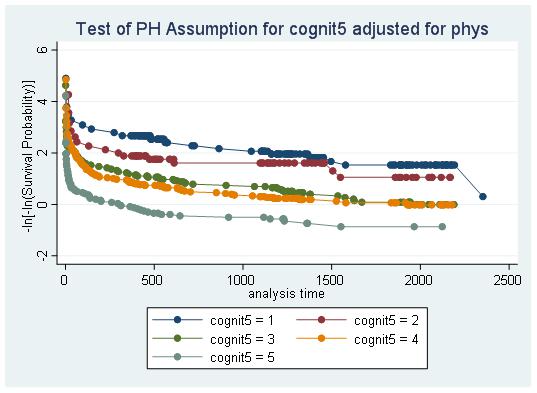
b)
There are crossing curves when cognit5=3 and cognit5=4 (not parallel). Thus, the PH assumption is violated, seeming to be non-linear. I suggest to decrease the quantile numbers for cognit, so that the 60th and 80th can be in the same group, eliminating the crossing line.
c)
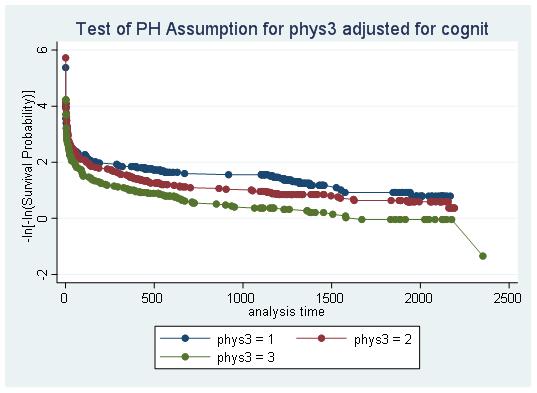
d)
There are crossing curves when phys3=1 and phys3=2 (not parallel). Thus, the PH assumption is violated, seeming to be non-linear. I suggest to decrease the quantile numbers for cognit, so that the 33.3th and 66.7th can be in the same group, eliminating the crossing line.
e)
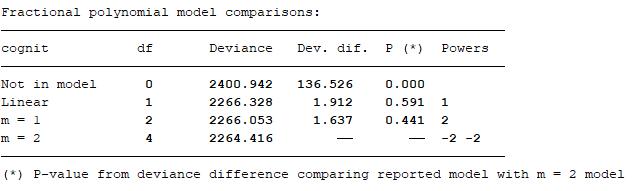
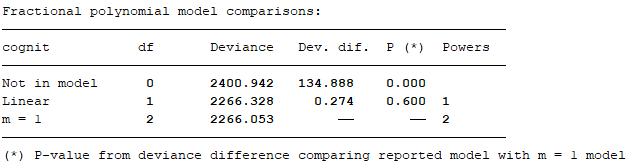
The fractional polynomial model tests suggest that the degree (2) model is no better than degree (1) and that the degree (1) model is no better than linear. The hypothesis tests carried out include:
degree (1) model is sufficient and best degree (2) model is no better than best degree (1) model;
linear function is suitable and best degree (2) model is no better than linear model;
cognit has no effect and best degree (2) model is no better than null model;
linear function is suitable and best degree (1) model is no better than linear model;
cognit has no effect and best degree (1) model is no better than null model;

更多其他:prensentation代写 文学论文代写 商科论文代写 艺术论文代写 人文代写 Case study代写 心理学论文代写 哲学论文代写 计算机论文代写



您必须登录才能发表评论。