中级计量经济学代写 经济学代写

Intermediate Econometrics

中级计量经济学代写 This exam contains 5 pages (including this cover page) and 4 problems. Check to see if any pages are missing. Enter all requested…

This exam contains 5 pages (including this cover page) and 4 problems. Check to see if any pages are missing. Enter all requested information on the top of this page, and put your name on the top of every page, in case the pages become separated.

You may use your books, notes, or any sources on this exam. 中级计量经济学代写

You are required to show your work on each problem on this exam. The following rules apply:

• If you use a “fundamental theorem” youmust indicate this and explain why the theorem may be applied.
• Organizeyour work, in a reasonably neat and coherent way, in the space provided. Work scat- tered all over the page without a clear ordering will receive very little credit.
• Mysterious or unsupported answers will notreceive full credit. A correct answer, unsup- ported by calculations, explanation, or algebraic work will receive no credit; an incorrect answer supported by substantially correct calculations and explanations might still receive partial credit.
• Ifyou need more space, use the back of the pages; clearly indicate when you have done this.

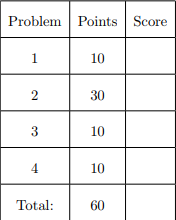
Do not write in the table to the right. 中级计量经济学代写

1. (10points) Basic

(a) Consider a multiple linear regression model that is assumed to follow the assumptions 1-MLR.6:

y_i = β₀ + β₁x_i,1 + β₂x_i,2 + β₃x_i,3 + ϵ_i, ϵ_i ∼ N (0, σ²)

Please classify the elements of this model into the three categories ‘parameters’, ‘observed variables’, ‘unobserved variables’, approximately as follows: ‘Parameters: · · · ; Observed variables: · · · ; Unobserved variables: · · · .

(b) Which of the conditions 1-MLR.6 are required for the BLUE property, i.e. which of them are the Gauss-Markov assumptions?

(c) Suppose now that the model is really a model for time-indexed data, but that it is  List the Gauss-Markov conditions for this type of model.

(d) When a regression model called dynamic? 中级计量经济学代写

2. (30points) Suppose we have the following model

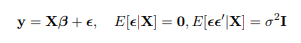
where X is n × (k + 1) such that X^rX is non-singular. The OLS estimator for β is

(a) 1.Show that the OLS residuals can be written as sˆ = M s where M  = I_n×n−X(X^rX)^—1X^r.

2. Show that 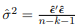   is an unbiased estimator for σ².
3. Show that
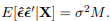
4. Show that 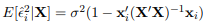where x^r is the i-th row of the matrix X.

(b) Explain why the following relationship holds 中级计量经济学代写

y^ry = y^rX(X^rX)^—1X^ry + sˆ^rsˆ

(c) The expression  x^ri(X^rX)^—1x_i  in  part  (4)  is  often  denoted  by  h_i,  and  it  is  useful  for highlighting influential observations. In particular, it can be shown that

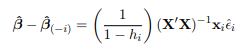
where βˆ(-i) is the OLS estimator for β when the i-th observation is omitted

1. Show that 0 < h_i <  (Hint: consider a regression of e_i on X, where every element of the n × 1 vector e_i is zero except for the i-th element, which is one.)
2. Show that h_i has an average value of

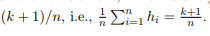
3. (10points) Heteroskedasticity 中级计量经济学代写

(a) Suppose there is heteroskedasticity in a simple regression model y_i= β₀ + β₁x_i + ϵ_i, thus violating one Gauss-Markov condition, while all other such conditions  Will OLS be unbiased and consistent?

(b) Suppose the form of this heteroskedasticiy is known as σ² = γ²x². How can you use the idea of ‘weighted least squares’ to specify a regression that fulfills all Gauss-Markov conditions and can be estimated efficiently by OLS?

4. (10 points) For each of the following tests, write down the null hypotheses, the alternativehypotheses, and the (maybe asymptotic, if an exact distribution does not exist) distribution of the test statistic under the null. You can use words or symbols, but unusual notation must be explained.

(a) The Breush-Pagan test; 中级计量经济学代写

(b) The t-test for the third regression coefficients;

(c) The F-test for the last two regression coefficients in a regression with 4 regressors.