偏微分方程代写 DIFFERENTIAL EQUATIONS

PARTIAL DIFFERENTIAL EQUATIONS AND VECTOR CALCULUS B

偏微分方程代写

Answer THREE of the FOUR questions.

If more than three questions are attempted, then credit will be given for the FIRST THREE answers.

Answer THREE of the FOUR questions.

If more than three questions are attempted, then credit will be given for the FIRST THREE answers.

Electronic calculators may be used, provided that they cannot store text.

1. 偏微分方程代写

a) Showthat the eigenvalues of the eigenvalue problem

X′′ (x) − λX(x) = 0, 0 < x < 1,

(where X′′ (x) denotes the second derivative of X(x) with respect to x), subject to the boundary condition

X(0) = 0, X^r(1) = 0,

are

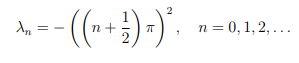
Find the corresponding eigenfunctions X_n(x), n = 0, 1, 2, . . .

[8 marks]

 

b) Using the method of separation of variables, and your answer to part a), show that the solution u(x, t) to the one-dimensional heat equation

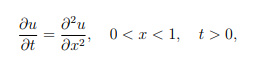
subject to the boundary conditions

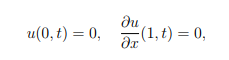
and the initial condition u(x, 0) = f (x), can be written in the form

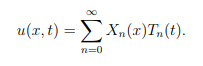
Determine expressions for X_n(x) and T_n(t) and give integral expressions for any arbitrary constants. Show ALL steps in your calculation but do not evaluate any integrals. (You may assume without proof that the eigenfunctions X_n(x) are orthogonal on the interval [0, 1].)

[12 marks]

 

2. 偏微分方程代写

a) Show that the function

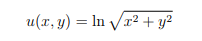
is a solution to Laplace’s equation

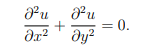(1)

[4 marks]

b) Use the chain rule for partial derivatives to show that

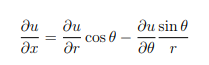
where r, θ denote the usual polar coordinates. Using this expression, and applying the chain rule again,derive an expression for
in terms of the derivative

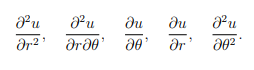
[12 marks]

c) Laplace’s equation (1), rewritten in polar coordinates is 偏微分方程代写

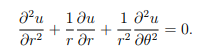(2)

Convert the function  into a function in polar coordinates and show that it satisfies Laplace’s equation (2) in polar coordinates.

[4 marks]

3.We want to approximate the solution u(x) of the convection-diffusion equation:

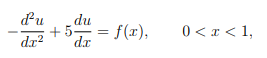
subject to the boundary conditions 偏微分方程代写

u(0) = 1, u(1) = 0.

Let U_j denote an approximation to u(x_j), where x_j = jh are uniformly spaced grid points, with j = 0, 1, . . . , N and

a) Define the first centered finite difference δu(x_j)at a point x = x_j and derive the second centered finite difference δ²u(x_j). Hence derive the following approximation to the second derivative:

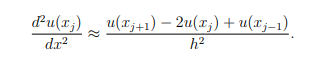
[4 marks]

 

b) By combining the following approximation

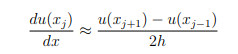
with the one given in part a), derive the following finite difference scheme for the convection-diffusion equation

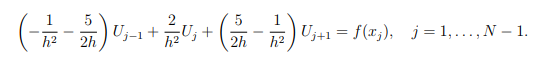
State the boundary conditions that the approximations must satisfy.

[4 marks]

c) Choose N = 4 intervals and let f = 1. Derive (but do not solve) the linear system of equations that must be solved to obtain the approximations U₁, U₂, U₃.

[3 marks] 偏微分方程代写

d) Define the term truncation errorT_j at a point x_j and show that, using suitable Taylor series expansions,

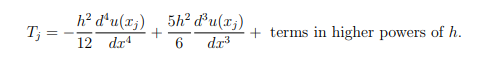
[9 marks]

4.

a) For the scalar function g(x, y, z) = x + 3y²z + 2y and the vector function G = 2zy²i + zj + 3xyk, calculate the gradient ∇g, and the curl ∇ × G.

[4 marks]

b) Prove that, for any scalar function f = f (x, y, z), ∇ × (∇f ) = 0. 偏微分方程代写

[4 marks]

c) Byusing spherical coordinates show that

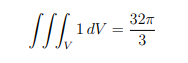
where V denotes the sphere of radius two, centered at the origin.

[5 marks]

d) Use the standard formula to construct a unit vector nˆ that points in the outward normal direction to the surface S of the sphere in part c). Hence, evaluate the surface integral

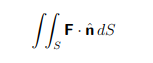
where F = xi + yj + zk. (You may use without proof the standard formula for the surface area of a sphere.) 偏微分方程代写

[4 marks]

e) State the Divergence Theorem and, using your answers to parts c) and d), show that it is satisfied for the vector function F = xi + yj + zk, where V is the volume enclosed by a sphere of radius

[3 marks]