6CCM318A Fourier Analysis
傅里叶分析代写 This paper consists of two sections, Section A and Section B. Section A contributes 50% of the total marks for the paper.
Summer 2020
Time Allowed: Two Hours
This paper consists of two sections, Section A and Section B. Section A contributes 50% of the total marks for the paper.
Answer all questions in Section A and all questions in Section B. All questions in Section B carry equal marks.
NO calculators are permitted.
DO NOT REMOVE THIS PAPER FROM THE EXAMINATION ROOM
TURN OVER WHEN INSTRUCTED
SECTION A 傅里叶分析代写
A 1. Let f : S1 → C be an integrable function.
- Define the Abel sums (Ar(f ))() related to f , r > 0, and the Poisson kernel Pr(θ). State without a proof whether {Pr(·)}0≤r<1 is a family of good kernels as r → 1−. [3 marks]
- Prove that the Fourier series of f is Abel convergent to f at all points of continuity θ ∈ S1 of f . You may use the Good Kernels theorem, provided you state it [7 marks]
- For each of the following statements determine whether it is true or Justify your answers with a proof or a counterexample.
(i) If f is continuous everywhere on S1, then the Abel convergence of the Fourier series of f is
(ii) The Fourier series of f is Abel convergent to f 傅里叶分析代写
(iii) If a series of numbers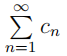 
is Abel convergent to s, then it is also convergent to s in the usual sense.
(iv) If the Fourier series of f converges uniformly to f , then it is also uniformly Abel convergent to f . [15 marks]
A 2. (a) For Schwartz functions f, g ∈ S(R) define the convolution (f ∗ g(·) and state without a proof whether f ∗ g ∈ S(R). Does f^∗ g(·) make sense? [3 marks]
(b) Provethat if f, g ∈ S(R) are Schwartz functions, then
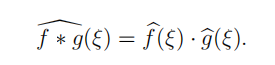
[7 marks]
(c) For each of the following statements determine whether it is true or Justify your answers with a proof or a counterexample.
(i) f(x) = e−|x| is a Schwartz function. 傅里叶分析代写
(ii) f(x) = e−x4 is a Schwartz function.
(iii) If f, g ∈ S(R) are Schwartz functions, then
(F∗f ) · (F∗g) = F∗(f ∗ g).
(iv) If f, g ∈ S(R) are Schwartz functions, then f g ∈ S(R).
(v) If f, g ∈ S(R) are Schwartz functions so that for all x ∈ R, g(x) > 0, then f (x)/g(x) ∈ S(R). [15 marks]
SECTION B 傅里叶分析代写
B 3. Let f : S1 → C, f (θ) = |θ| on θ ∈ [−π, π].
(a) Evaluate the Fourier coefficients f (n) of f and hence find the Fourier series of f in its complex and its real forms. [15 marks]
(b) Use your answers to part (a) to determine whether the Fourier series of f converges to f , and whether it converges uniformly to f w.r.t. x ∈ S1. [5 marks]
(c) By computing the Fourier coefficients of g := f ∗ f find a maximum possible k ≥ 0 so that g ∈ Ck(S1). [5 marks]
B 4. Let f : R → C be the function
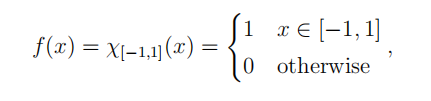
i.e., the characteristic function of the unit interval in R.
(a) Evaluate the Fourier transform of f , and use your result to compute the Fourier transform of the function f (x) = sin x . [12 marks]
(b) Find the convolution g(x) := (f ∗ f )(x) of f with itself, and its Fourier transform f (ξ). (Hint: you are not required to compute the Fourier transform of g directly.) [7 marks]
(c) By applying the Plancherel identity or otherwise, evaluate the integral
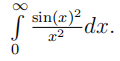[6 marks]
