中国代考_先进微型 – Advanced Micro II – 考试代写

Advanced Micro II

Final Exam Winter 2021

先进微型 Are the following statements True, False, or Uncertain? Whatever your answer, to get credit you must provide a justification.(5 points)

Welcome! You will have 120 minutes to RETURN this test. The test is worth 110 points, so plan your time so that you spend one minute per point, with 10 minute buffer to return the test. You will get partial credit so it is very costly to leave a question completely blank. The points per question are listed in parentheses. POINTS WILL BE DEDUCTED HEAVILY IF YOU TURN THE TEST IN LATE.

1 True, False, or Uncertain  先进微型

Are the following statements True, False, or Uncertain? Whatever your answer, to get credit you must provide a justification.

1. (5 points) If Jack has expected utility preferences over lotteries, then a positive linear transformation of his expected utility function still has the expected utility form and preserves the same
2. (5 points) Suppose there are two  groups,  A and B, where the population mean of group A is below    that of group B but the population variance of both groups is the same. Statistical discrimination negatively affects the wages of above average members of group A but positively affects wages of below average members of group A, relative to what they would receive if the only thing we changed about themwas which group they belonged
3. (5 points) Suppose an individual is considering his preferences over the set of lotteries which yield one donut with some probability and otherwise yield a cup of coffee.  If coffee and donuts are substitutes     in his consumer preferences, he will act less risk averse over these lotteries than if coffee and donuts were
4. (5 points) A possible way to keep insurance companies from cream skimming is to make laws which dictatewhat insurance must cover (how large A must be, in our classroom notation).
5. (5 points) When you apply for life insurance,  you are required to pass a physical exam primarily  because the insurer wants to prevent moral
6. (5points) The risk premium of a lottery cannot exceed the expected value of a lottery

2 Problems  先进微型

1. (15 points total) A risk-averse individual would prefer to receive $100 than to enter a lottery L₁in   which he gets $200 with probability 0.5 and $0 with probability .
   • (2points) Suppose now this person is offered a lottery which gives him $100 with probability

.99, $200 with probability .005 and $0 with probability .005. Call this lottery L₂. What is the expected value of this lottery?

• (4points) What can we say about his preference for L₂ compared to receiving $100 with certainty?
• (9 points) Suppose that the preferences underlying his choices satisfy independence. What can we say about his preference for L₁compared to L₂?

2. (25 points total) Consider the Rothschild and Stiglitz model of insurance discussed in class. In partic- ular,assume that people in the economy have the same wealth W and each face a potential loss of size

1. However,individuals vary in their probability of experiencing this loss:  先进微型

2. A fraction λ are high risk  and have a probability p^Hof a loss, while a fraction 1  λ are lower risk and have a probability p^L < p^H of a loss. Assume that the probabilities are private information to the agent. Agents maximize their expected Suppose that there exists a competitive insurance market that consists of insurance companies attempting to maximize expected profit by providing insurance contracts. Recall that in equilibrium, no offered contract makes negative expected profits and no un-offered contract could make a positive expected profits.
   • (10 points) Graphically depict the only type of contracts offered in equilibrium. You may assume that λ is such that an equilibrium exists. Be sure to at minimum label 1) the uninsured endowment of wealth across states 2) the 2 agent’s indifference curves 3) the zero profit line(s) and 4) the equilibrium.
   • (5 points) Is this equilibrium Pareto efficient?

• (10 points) Now suppose that the high risk individuals become less risk averse (but are still risk- averse). 先进微型

• What does the new equilibrium look like compared to what we saw in (a)? If there is an equilibriumin (a), is there necessarily an equilibrium in this new market?

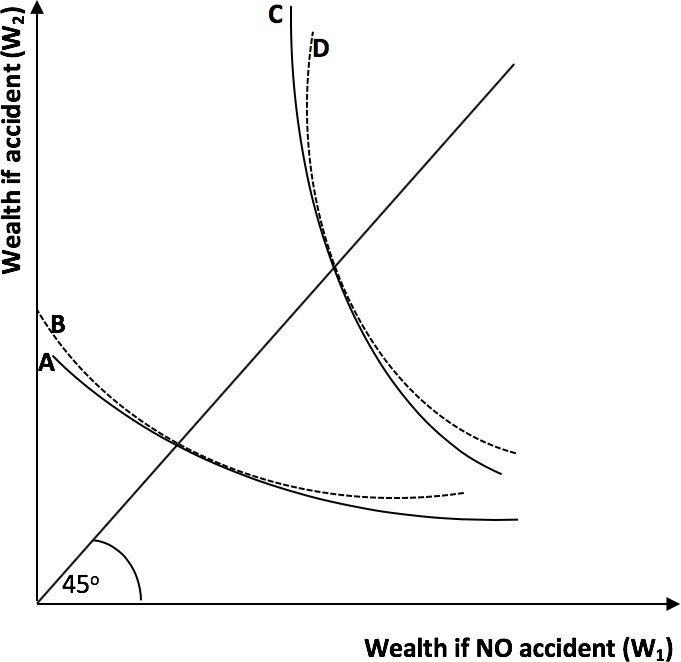
3. (20 points total) Consider the graph below.   It displays 4 indifference curves over  wealth in case a car accident happens vs. in case a car accident does not happen. The 4 indifference curves represent preferences of 4 different individuals. Each of whom has the same endowment without insurance. Zed and Wyatt both have the same probability of being in a car accident. But Wyatt is more risk averse than Zed. Yona and Xerxes also have the same probability of being in a car accident. But this probability is higher than that of Wyatt and Zed. Xerxes is more risk averse than Describe which indifference curve (A,B,C, or D) belongs to each individual (Zed, Wyatt, Xerxes, and Yona). Explain each of your four answers for fullcredit.

4. (20 points total) Scott hires a real estate agent named Travis to help him sell his house.

5. The expected sales price is 2e, where e is Travis’ effort (so more effort results in a higher sales price). Effort costs Travis e²/ Scott proposes a compensation contract, Travis decides whether or not to accept  the contract. And then Travis chooses how much  effort he puts into selling Scott’s home.  Assume that  Travis and Scotts’ outside options are0.
   • (10 points) Real estate agents are paid on commission.  That is, Travis’  contract with Scott says  that he will get a fraction x of the total sales price of Scott’s home as payment.  What is the   optimalx^∗ from Scott’s perspective? What is the optimal effort e^∗ from Scott’s perspective?
   • (5 points) What is Travis’ effort e^∗when he sells  his  own  house  (he  doesn’t  hire  a  real  estate  agent, and his expected sales price is 2e where e is his own effort which costs e²/2)?
   • (5 points) Suppose Scott could charge Travis some fixed price for selling his home (so the contract could also include a fixed fee). How much would hecharge?

更多其他：环境学代写 政治学代写 数学代写  生物学代写 统计代写

合作平台：天才代写 幽灵代写  写手招聘  paper代写