AMATH 250 Online Assignment 5
函数代考 Late penalty is 1% per hour. It is your responsibility to make sure you have time to upload your assignment by the deadline.You…
Late penalty is 1% per hour. It is your responsibility to make sure you have time to upload your assignment by the deadline.You may use the course materials posted on the course website and the optional text as references. You are also allowed to discuss ideas with your classmates, the course instructor and TAs. Please do not post fifinal answers or give away too much on Piazza; it will be monitored closely. Your submitted work must be written upon your own and should indicate your knowledge of the material.
Academic Integrity Declaration (AID): Fill out the Academic Integrity Declaration form and upload as a page 1 to Crowdmark. 函数代考
I declare the following statements to be true:
- The work I submit here is entirely my own
- I have not used any unauthorized aids
- I am aware that misconduct related to examinations can result in signifificant penalties including failing the course and suspension, as outlined in Policy 71
- I have discussed the assignment with the following people (if any):
- Write your name and the date in the box below, then upload this page to Crowdmark.
Each question should be uploaded separately to Crowdmark. 函数代考
- Consider the model for a rocket launched from the surface of the earth subject only to the force of gravity
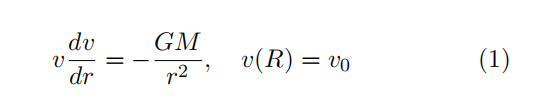
(1) Here v is the velocity of the object, r is the distance of the object from the centre of the earth, G is universal gravitation constant, M is the mass of the earth, R is the radius of the earth and v0 is the initial velocity. In this problem, we will consider a di↵erent way of determining dimensionless variables.

Make sure your choices ensure that x and w are dimensionless.
(d) Give the expression for the dimensionless constant w0. What does this represent physically?
- Consider a pendulum, with rope length l and weight with mass m. Let the force of gravity be g. Assume the pendulum is started from an initial angle of ✓. Use M as the mass unit symbol, L as the length unit symbol, and T as the time unit symbol.
(a) Use the Buckingham Pi theorem to fifind an expression for the maximum angular velocity v?
Does this expression depend on the mass? 函数代考
Note: Angles are dimensionless. Angular velocity is measured as angle per time, with units 1/T
(b) Now consider the maximum tangential velocity v (this has the more standard units for speed of length per time; L/T ). How does your expression change?
- Nondimensionalize the equation:
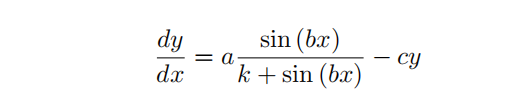
Note: You don’t actually need to know the dimensions of x and y to do this; just let [x] = X and let [y] = Y . Also, the arguments to transcendental functions and their output are always dimensionless.




