FX COMPUTER ASSIGNMENT
利率代写 Below are quoted volatility data for short-dated options on XXXYYY, as of 03/09/2022. The spot rate is 1.445; you may ignore settlement delays.
DUE ANYTIME BEFORE FINAL EXAM 利率代写
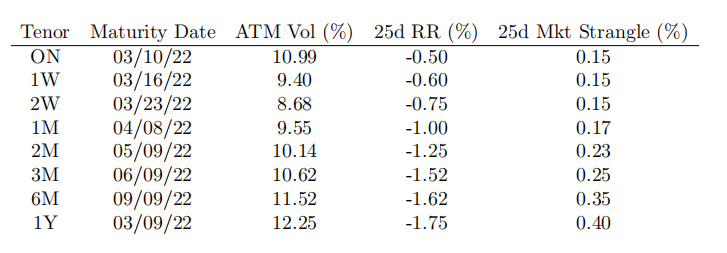
Below are quoted volatility data for short-dated options on XXXYYY, as of 03/09/2022. The spot rate is 1.445; you may ignore settlement delays. Assume that the (continuously compounded) XXX and YYY interest rates are 1% and 2%, respectively.
Q0: As warm-up, implement the SABR formula for implied volatility and replicate the graph in Appendix of lecture 3. Show the graph in your answer.
Q1: For every maturity in the table, use the SABR model (with correlation parameter ρ set to 0), to construct all 5 strikes involved in the market quotes. For every maturity, list these strikes and their corresponding implied volatilities (make a nice table). In a separate table, list the calibrated SABR parameters for every maturity.
Q2: For the 3-month (3M) maturity, work out the strikes that correspond to deltas of 10% and 90%. On this range of strikes, draw a smooth graph of the function σ(K). 利率代写
Q3: List the implied volatility when the strike is equal to the forward rate, for all maturities in the table.
Q4: We want to use the event-weighting scheme of Lecture 3 to take into account week-end effffects (ignore holidays and other events); assume that volatilities are set to 0 on weekends. Given this, and ignoring the smile, use the ATM-forward volatilities in Q3 to construct implied volatilities for every day (including weekend days) out to the 6-month maturity point (should be around 180 separate dates). Draw a graph of these volatilities as a function of option maturity. As in the lecture notes, assume that the function q is piecewise flflat.



