北美MATH作业代写 变量代写 函数代写

MATH作业代写

北美MATH作业代写 因变量：R₁(t) 自由变量：j、μ_θ、μ_k、μ_k0、σ_θ²、σ_k0²、σ_k²、σ²t 常量：a_th、λ

μ_θ、σ_θ² 正态函数的均值和方差 μ_k、σ_k²正态函数的均值和方差 μ_k0、σ_k0²正态函数的均值和方差 σ²服从布朗运动

做出一条可靠性与加载次数的曲线。。。

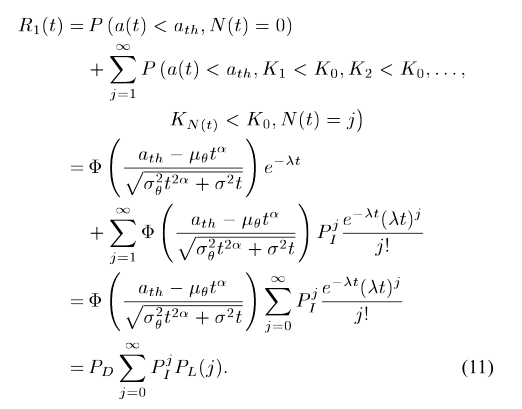
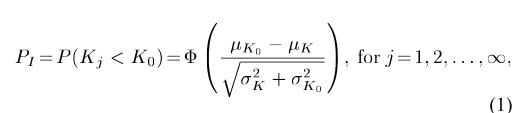
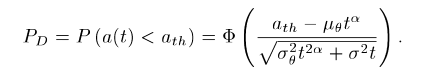
因变量：R₁(t)

自由变量：j、μ_θ、μ_k、μ_k0、σ_θ²、σ_k0²、σ_k²、σ²t

常量：a_th、λ

μ_θ、σ_θ² 正态函数的均值和方差

μ_k、σ_k²正态函数的均值和方差

μ_k0、σ_k0²正态函数的均值和方差

σ²服从布朗运动

做出一条可靠性与加载次数的曲线，类似于这种。标黄色的部分，做完可靠性曲线以后做一个灵敏度分析。

a_th是裂纹长度

a(t)是裂纹扩展速率 北美MATH作业代写

N（t）代表寿命周期内过载的总次数，(N（t），t>0)~P(λ)

Kj断裂韧度值~N(μ_k、σ_k²)

K0裂纹萌生韧度值~N(μ_k0、σ_k0²)

一个正态随机变量Θ~ N(μ_θ、σ_θ²)

α 是一个常数

方差σ²t服从布朗运动，均值为0

λ 是泊松分布的的参数，代表的是单位时间内过载发生的次数

灵敏度分析 北美MATH作业代写

分析λ

用蒙特卡洛法去量纲分析μ_θ、μ_k、μ_k0、σ_θ²、σ_k0²、σ_k²、σ²t的灵敏度