多元回归分析代写 Regression Analysis

多元回归分析代写 Lecture 1: Multivariate Regression Analysis

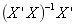
多元回归分析代写 Under these assumptions we have the ordinary least square (OLS) estimator:The matrix  is often referred to as the projection matrix…

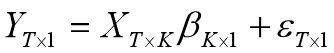
Unknown parameters:

Assumptions: 

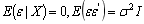1. (Note 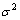is constant)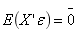
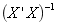
2. 
3. 

Under these assumptions we have the ordinary least square (OLS) estimator:

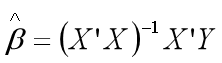
The matrix  is often referred to as the projection matrix

Sampling properties of the OLS estimator: 

1. we look at the property of unbiasedness for 

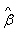
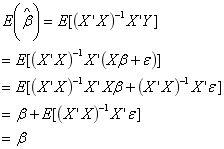
2. The variance-covariance matrix for 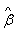is given by  

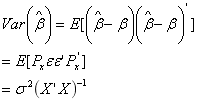
      Given the unbiased property, the next question concerns comparison with other linear unbiased estimator. The Gauss-Markov theorem states: 

Thus,  BLUE

Having obtained a point estimator for the unknown parameter  , we now turn to estimating

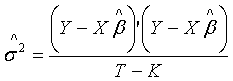
Where T is the number of observations and K is the number of explanatory variables. 

 is an unbiased estimator for

t-value=

Summary:  多元回归分析代写

• First, calculate
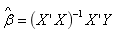
• Second, using the estimated 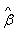, calculate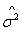
• Third, generate t values for each parameter
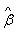
• Finally, analysis your results.