微分方程代写 Vector Calculus And Differential Equations

Vector Calculus And Differential Equations

微分方程代写 Most of the formulas and theorems provided are stated without the conditions under which they apply. The notation used is the same…

Formula Sheet 微分方程代写

Most of the formulas and theorems provided are stated without the conditions under which they apply. The notation used is the same as that used in lectures.

 

Curve

For a given curve C in R³ with parametrization α : [a, b] → R³,

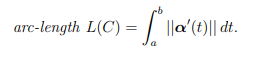
Line Integrals 微分方程代写

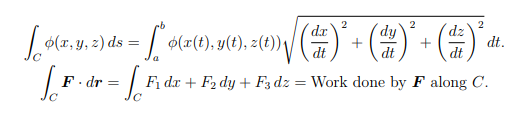
Grad

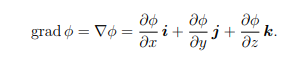
∇φ is normal to the tangent plane of the level surface {φ(x, y, z) = k} for a constant k. If F = ∇φ for some smooth φ, then F is conservative, φ is a potential function of F, and F · dr is path-independent.

 

Curl 微分方程代写

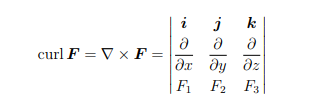
If the domain of F is simply connected (irrelevant for the requirement of MATH2021) and ∇ × F = 0, then F is conservative.

Double Integral

 

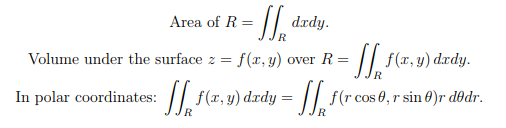
Divergence

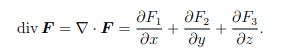
Green’s Formula (Theorem) 微分方程代写

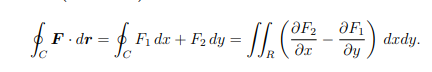
Using ”curl = ∇×”,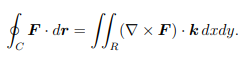

Divergence Theorem in 2D

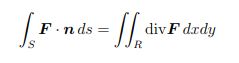
Surface Integral 微分方程代写

S is the graph of z = f (x, y) for (x, y) in R. Then

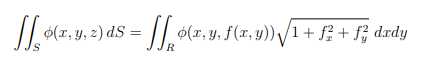
Flux across S =

Triple Integral

In cylindrical coordinates:

∫∫∫ f (x, y, z) dxdydz = ∫∫∫ f (r cos θ, r sin θ, z) r drdθdz.

In spherical coordinates:

∫∫∫ f (x, y, z) dxdydz = ∫∫∫ f  r cos θ sin ϕ, r sin θ sin ϕ, r cos ϕ  r² sin ϕdrdθdϕ

Gauss’ Theorem: Divergence Theorem in 3D 微分方程代写

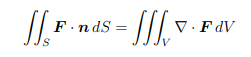
Stokes’ theorem

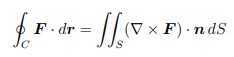
Fourier Series

For a 2L-periodic function f : R → R, the Fourier series of f : 微分方程代写

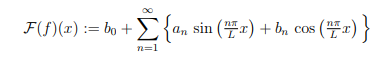
where the Fourier coefficients b₀, (b_n)_n≥1 and (a_n)_n≥1 are given by

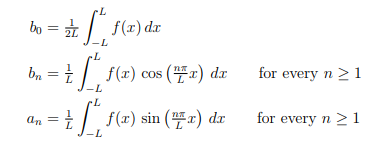
Table of Standard Integrals 微分方程代写

 

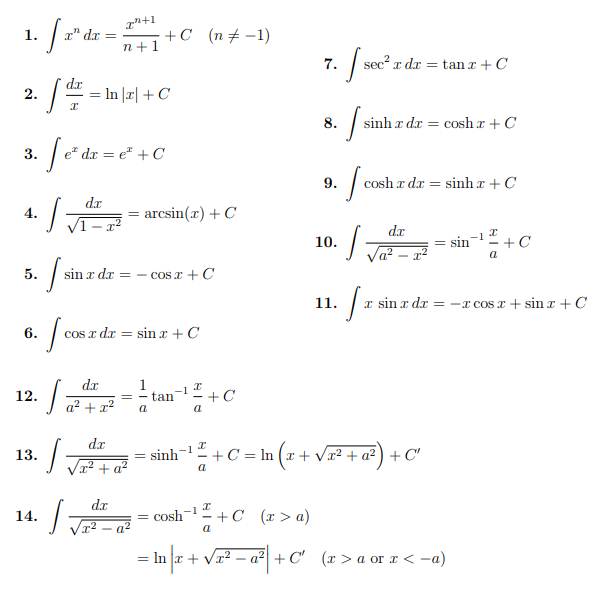
Instructions

• Open book.
• Show all necessarywork, which will be marked.
• Thereis no need to print out the question paper,
• Writeby hand on paper, and scan for online submission.
• Include SID in submission.

1. Thefollowing questions are considered in the xy-plane, R².

(a) Find the parametrisation α(s) for the unit circle S₁= (x, y) x² + y² = 1 , where s is the arc length parameter and the direction is counter-clockwise. Make sure to specify the range of s. 微分方程代写

(b) There is a very thin metal ring in the shape of S₂= (x, y) x² + y² = 4 . Under the parametrisation β(t) = (2 sin t, 2 cos t) for t  (   π, π], the density of it is 2 + sin t. Calculate the total mass of the ring.

(c) Usingthe definition of curve/line integral, calculate

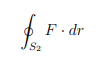
where S₂ = {(x, y) | x²+y² = 4} with the parametrisation β(t) = (2 sin t, 2 cos t) for t ∈ (−π, π] and the vector field F (x, y) = (y, −x).

(d) Applying Greens’ Formula/Theorem, calculate the curve/line integral in (c) by translating it first to a double integral.

(e) Justify that the vector field G(x, y) = (x, y) is conservative, and the vectorfield F (x, y) = (y, −x), already in (c), is not conservative.

(f) Using polar coordinates, calculate the double integral 微分方程代写

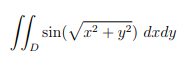
where D = {(x, y) | x² + y² ≤ 1}.

2. Thefollowing questions are considered in the xyz-space, R³.

(a) Consider the planex + 2y + 3z = 10 as a graph over the xy-plane. By surface integral, calculate the area of the part of the plane over the triangle in the xy-plane, with vertices (0, 0), (1, 0) and (0, 1).

(b) For the vector field F (x, y, z) = (xy², yz², zx²) and the unit sphere S = calculate the flux of F through S in the

outward direction by Gauss’ Theorem.

(c) For the same vector field F (x, y, z)  =  (xy², yz², zx²) as in (b),  calculate ∇ × F .

(d) For the vector field F (x, y, z) = (xy², yz², zx²), calculate the flux ofF through the unit lower hemisphere H = (x, y, z)  x² +y² +z² = 1, z  0  in the direction which goes into the unit ball B = (x, y, z) x² + y² + z² 1 by Stokes’ Theorem.

3. Thisquestion is on solving  微分方程代写

(a) Find the particular solution for the unknown y(x):

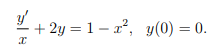
• Find the particular solution for the unknown y(x):

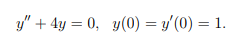
• Find the particular solution for the unknown y(x):

• Find the general solution for the unknown y(x):

by the method of Variation of Parameters.

• Find the general solution for the unknown y(x):

for x ∈ [−π, π] using Fourier series.

• Findthe particular solution for the unknown y(x):

using Laplace Transform.