MATHS 260
MATHEMATICS
Difffferential Equations
微分方程作业代写 Use the answer sheets provided at the back of the exam paper for your answers to Question 3 and Question 5. Spare copies of…
NOTE: This paper contains SIX questions. Answer ALL questions.
Use the answer sheets provided at the back of the exam paper for your answers to Question 3 and Question 5. Spare copies of the answer sheets are available if you need them.
Show ALL your working.
There are 100 marks in total.
-
(12 marks) 微分方程作业代写
(a) Find a solution to the initial value problem
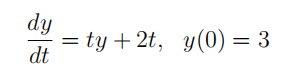
(b) Could there be any other solutions to this initial value problem? Explain your answer carefully.
- (10 marks) The fifigure below shows a bifurcation diagram for a difffferential equation
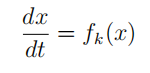
where k is the bifurcation parameter.
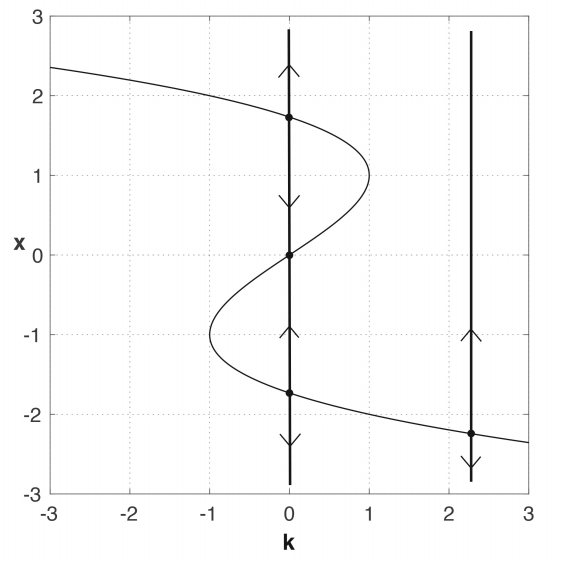
(a) Find all values of k for which there is a bifurcation.
(b) Describe the long term behaviour of the solution to the difffferential equation if:
(i) k = 0 and x(0) = 1; (ii) k = 0 and x(2) = 0; (iii) k = 2 and x(0) = −1.
(c) Sketch the phase lines for the cases: (i) k = −2; (ii) k = 1.
-
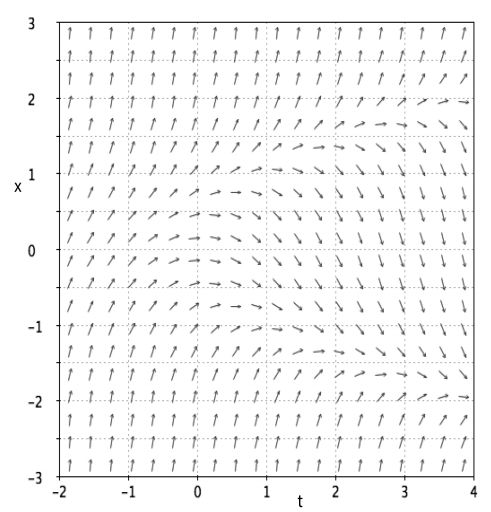
(12 marks) The fifigure below shows the direction fifield for a difffferential equation
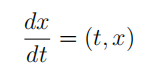
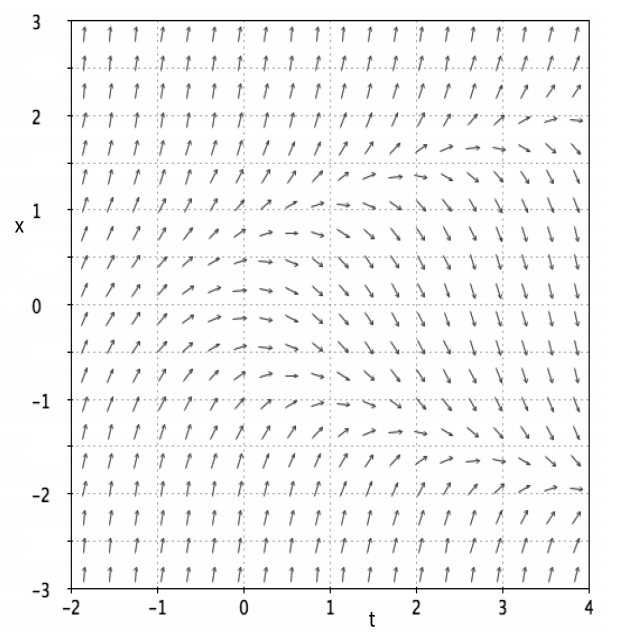
(a) On the answer sheet at the end of the question paper carefully draw the approx-imate solution that you would obtain if you used one step of Improved Euler’s method with step length h = 2 to calculate the solution to this difffferential equation with initial condition x(0) = 0. Note: You do not need to do any computations to answer this part of the question, but you should explain how you obtained your answer.
(b) On the second copy of the answer sheet at the end of the question paper, fifind the points in the (t, x)-plane where the direction fifield has zero slope, and write down a formula for a curve that goes through these points. Hence, write down a difffferential equation that might have been used to produce the direction fifield shown in the figure.
-
(22 marks) This question is about the system of difffferential equations 微分方程作业代写
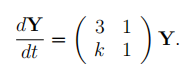
(a) Consider the case k = 0.
(i) Determine the type of equilibrium at (0, 0) (e.g., sink, spiral source).
(ii) Write down the general solution.
(iii) Sketch a phase portrait for the system.
(b) Now consider the case k = −3.
(i) In this case, the matrix has an eigenvalue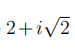 
with eigenvector 
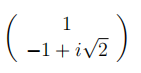and an eigenvalue 
with eigenvector 
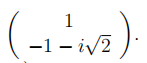Determine the type of equilibrium at (0, 0) (e.g., sink, spiral source).
(ii) Write down the general solution in terms of real-valued functions.
(c) For a given value of k the following phase portrait was produced. What value of k do
you think was used? Justify your answer. 微分方程作业代写
-
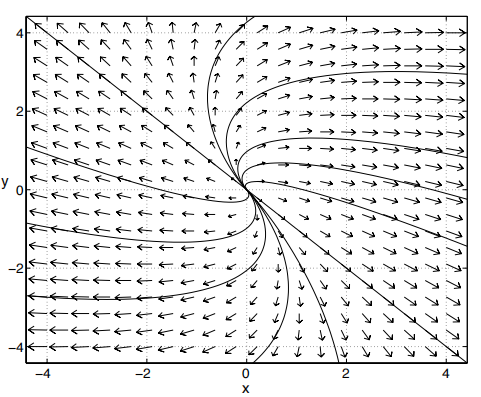
(26 marks) Consider the following system of equations:
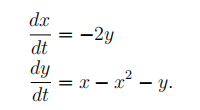
A grid is provided on the answer sheet attached to the back of the question paper. Use the grid for your answers to parts (b), (c), and (d) of this question.
(a) Find all equilibrium solutions and determine their types (e.g., saddle, spiral source). For each equilibrium that you fifind, draw a phase portrait showing the behaviour of solutions near that equilibrium.
(b) Find the nullclines for the system and sketch them on the answer sheet provided. Show the direction of the vector fifield in the regions between the nullclines and on the nullclines themselves.
(c) Sketch the phase portrait for the system on the answer sheet provided. Your phase portrait should show the behaviour of solutions near the equilibria, and should show some solutions in each difffferent part of the phase plane. Include the solution that satisfifies the initial condition (x(0), y(0)) = (0.5, 0).
(d) Describe the long-term behaviour (as t increases) of the solution with initial condition (x(0), y(0)) = (0.5, 0).
-
(18 marks) 微分方程作业代写
(a) A sailing boat is flfloating on the harbour. The following equation is used to measure the
vertical displacement, x, of the boat from its equilibrium position.
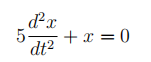
(i) Find the general solution to this difffferential equation.
(ii) Suppose that a storm results in a forcing function of the form f(t) = te−t , i.e. consider the model
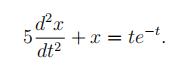
Find the general solution to this difffferential equation.
(b) A more general and realistic model for the motion of the boat is:
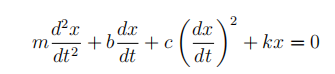
where m, b, c and k are positive constants.
(i) Brieflfly explain what each term in the equation might mean physically.
(ii) Rewrite this equation as a two-dimensional system of fifirst-order difffferential equations.
TIE THIS ANSWER SHEET TO YOUR ANSWER BOOK 微分方程作业代写
Answer sheet for Question 3(a)
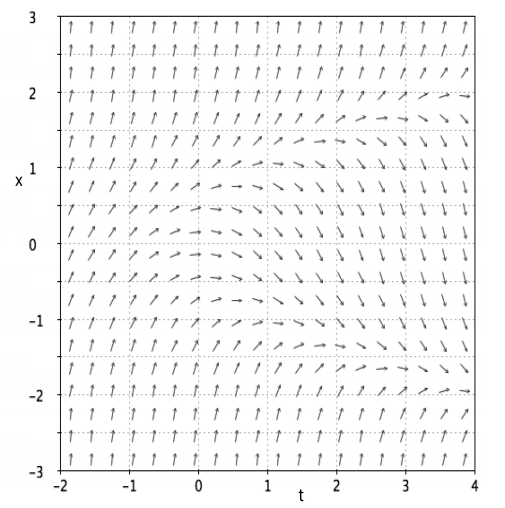
Answer sheet for Question 3(b)
Answer sheet for Question 5 微分方程作业代写
更多代写：project代写 多邻国代考 金融论文代写 经济代考 算法作业代写 商业分析代写
