MATH 102 Spring 2020
Homework 2
微积分代写 Instructions: You are welcome to discuss these problems with other students in the class and with the instructor. The work…
Instructions: You are welcome to discuss these problems with other students in the class and with the instructor. The work you submit, however, must be in your own words and reflect your own understanding of the problems.
These problems focus on applications of calculus, which means that your solutions are likely to involve written explanations (complete sentences), rather than only calculations. In your calculations and explanations, you must use correct notation. In particular, please label functions clearly: if you are calculating the derivative of a function g(x) then you should label it g(x).
Write complete solutions on your own paper; do not write your solutions on this paper.
Attach this cover page to your solutions. 微积分代写
Lecture Section (circle one): A01 A02
Name:
V00
1. [5pt] Recall from HW1 that we could model the number of internet users (measured in millions) in Canada by a logistic function:
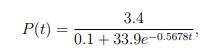
where t is the number of years after 1990. You found in HW1 that 微积分代写
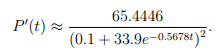
(a) In what year, according to this model, will the number of internet users grow the most?
(b) At what rate was the number of internet users growing in that year? (Or, if the year is in the future, at what rate will it be growing?)
2. [6pt] A lioness is hidden in the bush, 30 meters from a road. She sees an antelope stranded on the road, 10√21 meters away from her (see diagram below). Suddenly, she notices a jackal trying to get to the antelope from afar. The lioness starts running– she needs to get to the prey before the other predator does!
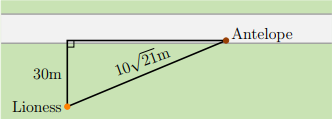
The lioness can run in the bush at a rate of 40 km/hr, and can run along the road at a rate of 80 km/hr. For example, if she runs straight to the antelope then she will run 10√21 meters at a rate of 40 km/hr:
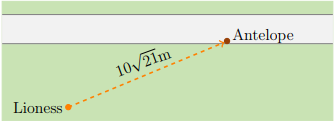
If she runs straight to the road, and then along the road to the antelope, she will run 30 meters at a rate of 40 km/hr, and then will run d meters at a rate of 80 km/h (you can calculate d by using the Pythagorean theorem for right triangles): 微积分代写
What is the shortest time in which the lioness can get to her prey and protect her family’s meal?
3. [5pt] Consider a cylindrical tree trunk of radius R. Living cells occupy a thin shell (thickness s) just inside the tree bark. The interior of the trunk consists of dead cells that have turned into wood.
(a) Let F be the fraction of the trunk volume that is living tissue.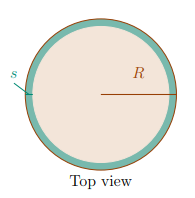
Find a formula for F that depends only on R and s. 微积分代写
(b) Notice that F and R both change with time as the tree grows,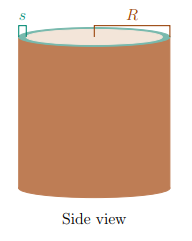
and assume thats does not change. Assuming that the radius of
the trunk grows at a constant rate of 2 millimetres per year, we
would like to know how F changes as the tree grows.
Compute 
, the rate of change of F, at the instant when the radius R is 10 times the thickness s.
(c) According to your calculation, is F increasing or decreasing at that moment?
(d) Suppose at some moment, = 0. What could you tell about the tree’s radius at that
moment? What would the tree look like?
4. [4pt] Suppose that for a certain textbook, the amount of revenue (in dollars) generated by selling q copies of the textbook is 微积分代写
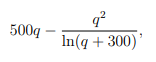
and the cost to manufacture q copies of the textbook is
100q + 100.
Then the profit function would be
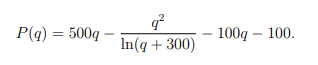
Recall that we can use differentials to estimate the change in profit: 
A new marketing campaign is expected to increase textbook sales by approximately 50 textbooks next month, but the campaign will cost $8,000. If the company currently sells 1000 textbooks per month, use differentials to explain why the marketing campaign is probably not a cost-effective idea.
Hint: you can use the the marginal cost and the marginal revenue formulas you calculated in HW1. Approximation. Here’s what we did last term, adapted to the textbook problem from HW1 this term.
