CARPOOLING AS A SOLUTION TO CONGESTION IN DUBLIN
By
Name
Course
Institution
Instructor
Location
City
Date
Carpooling as a Solution to Congestion in Dublin
Carpooling代写 The process of carpooling starts with the motive for car-sharing, communication of purpose between various agents, negotiation, and feedback.
Carpooling is one of the emerging method people are using to reduce the cost and time of commuting (Shaheen, Chan, and Gaynor, 2016, p. 168). The technique is eco-friendly and sustainable in terms of time saved, cost, resource use, and traffic congestion (Tahmasseby, Kattan, and Barbour, 2016, p. 241). Carpooling involves car-sharing between people going to similar or different destinations in a particular direction. The process of carpooling starts with the motive for car-sharing, communication of purpose between various agents, negotiation, and feedback. The goals for carpooling may be time-saving, convenience, cost of resources, and other constraints.
The paper will focus on the simulation model of carpooling with the Janus multi-agent platform. 各类北美代写
Essentially, it will simulate car-pooling where one agent traveling from point A to B so will put a request in the model which is also accessible by another person traveling in the same direction who will pool the same car. The model will tell how much time each of the agents takes to reach their destinations assuming in the same direction. Therefore, the model can be used to compare the time and cost taken by bus and car to travel the same route.

Geographical datasets, including accurate maps of Dublin, will be imported from GeoFabrik into Netlogo (Uri Wilensky , 1999), the platform where the agent-based model will be created. The scenarios of interest as a proof-of-concept for this research project include the following experimental setups:
- Users’ independently requiring travel from A to B evaluating both bus and carpool options according to each estimated time, costs –and, if applicable, how many would carpool.
- Different user picks up points, for example, if sharing with four people will it be four stops or everyone picked up from 1 stop or based on the location assigning closest pickup points for users.
The results of these simulations will be analysed to understand the feasibility of introducing a carpooling system in Dublin as a convenient way to travel across in Dublin and to explore the likely impact of carpooling implementation in transportation.
Carpooling Model Carpooling代写
An agent is an independent entity with autonomy in decision making on schedules and needs in traveling. The route schedule is the trips made in a certain period. The model used in this study considers socio-economic factors such as age, work, income, gender, education, relationships, vehicle, ownership, and among other sets of data inputs. The car-pooling model will be represented by:
TRL1 = {Unj=1 rqj, TTRL1}
Where,
TRL1 is the multiple stops car-pool has to stop
Rqj is the number of passenger requests
TTRL1 number of available cars for pooling in the system
The system manager (TRG) integrates all the information gathered from all operating cars for easy decisions about client pick-up point and most convenient car available for a given route. Carpooling代写
TRG = Unj=1 Infotj
Where Infotj is the information shared car-pooling and the system manager which include destination and preferences as shown below respectively:
Infotj = {Di, Pi}
Di = {D1,D2,……Dn}
Pi = {P1,P2,……Pn}
The system ensures cars-pooling work together and interacts to identify drop destinations and client mode choice. Each of the car-pooling has the objective of having a maximum number of trips in the city and transporting as many passengers as possible. The car goal can be modeled as Ntrips, which is between Nmin and Nmin + A. The number of trips made per day is dependent on time spent per trip and route traffic. These can be defined as the driver’s preferences. Carpooling代写
Nmin < Ntrip < Nmin + Λ
β∗Nmin = A
Where, β is the scalar value.
On the other hand, passenger’s objectives are to save time and hence have speculated upper and lower bound for the time to reach the destination. Tarrive defines time to spend to reach a destination using the most convenient route. Treach + λ is the latest time of arrival, and hence the change in passenger preference changes λ. Carpooling代写
Treach ≤ Tarrive ≤ Treach + λ ∗ Treach
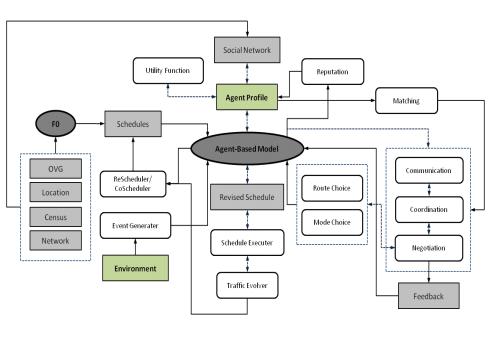
Figure 1: Agent-based Model for the Carpooling Application
Dublin Traffic Simulation in Netlogo Carpooling代写
i. Creation of Car
The main components of the programs are maps, cars, ways, and algorithms. Cars as the agent have distinct attributes and targets. They have identifications which make them differentiable from others. They are also differentiated in terms of association with passengers. The cars keep the records of trips made and time taken on each journey from the start to destination. The simulator provides users with an interface to select cars with a probability of selecting car-pooler provider. Carpooling代写
There are three car-pooler providers, including A, B, and C, which are selected with specific probabilities. The simulator will try to match the users with car-poolers, and hence, a new itinerary is created. The picks and drops depending on the number of passengers in the car. The maximum number of passengers is the car is 4 and when it is reached the car is not available in the pool. Below is the screenshot of the simulation.
The passenger’s options for the car-pooling is given by O = {O1, O2, … On} where O is the choice of car-pooling in n number of car-pooling in the city. The car choice is dependent on the destination and most convenient car available.
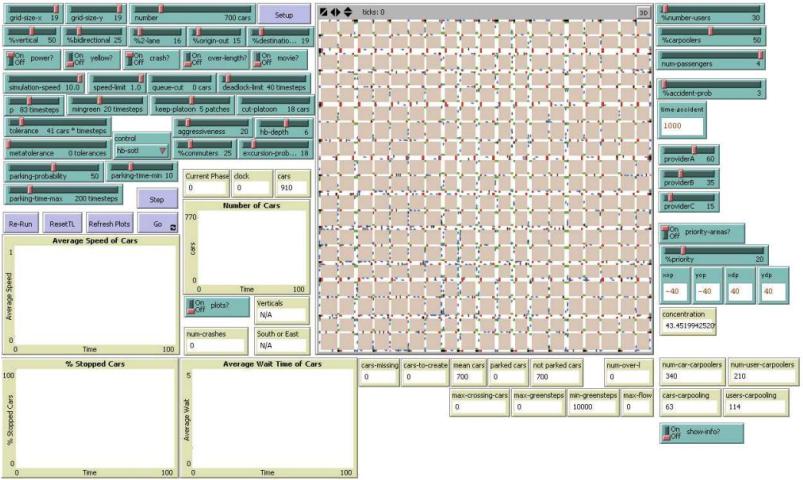
Figure 2: Screenshot of dynamic carpooling service simulator
ii. Creation of User
The user is the one seeking service from the car-poolers. The simulation needs to match the users with the most suitable service provider. The clients are identified using IDs as passengers present; time spends on the trip and distance. The cost depends on the number of passengers in the car.
iii. Simulation Algorithms Carpooling代写
The algorithm is used to match the clients with the most suitable driver. When the user requests for service, the system matches the user with a driver using the same direction. The possible cars are listed while the algorithm compares the user origin and destination to decide on the most suitable car to pool the user. When the user is assigned to the driver, the driver adds the passenger to the destination list. If there is no suitable driver, users will wait.
initialize: read in distance matrix, friction factors; allocate vehicle to stations; initialize vehicle parameters; initialize relocation parameters; generate trips; for time = tarrive to tarrive + λ { process event; update global parameter dataset; execute relocation process as necessary; } customer arrive event { calculate trip time; (to destination station) calculate energy to be used; if (vehicle available) { assign vehicle; execute vehicle departure process; } else queue customer; } vehicle arriveal event { process vehicle; reduce vehicle SOC; } Relocation arrival event { process vehicle(s) (reduce vehicle SOC) }
iv. High Populated Areas
Some parts in Dublin are highly populated while others have high demand as a destination. People are highly concentrated at the center of Dublin city compared to the outskirts. The area with a high population is simulated, as shown below.

Figure 3: Screenshot of the field with a high concentration
v. System Output
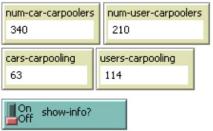
Besides other information displayed by the system, there are extra outputs with extra data. In figure 4 below shows, the “num-car-carpoolers” shows the number of carpoolers. The “cars-pooling” gives the number of cars available for trips. The “num-user-carpooling” indicates the number of users seeking services. The “users-carpooling” number of users matched with cars available.
Simulated Results Carpooling代写
The simulation assumed that users could afford trips, and there is an available car car-pooling. The results of the simulation will compare the normal trips where traffic jams are unavoidable with an ideal situation where time and distance covered will be compared. Therefore, the passenger choice for the car (O) is pegged on the trip characteristics.
The results show 15 parameters which are simulated under both conditions that are normal and ideal trips. Each scenario in the system takes 50 percent of cars. Each car has a capacity of 3 passengers. The map of the city and lanes used by the cars are similar. Also, the terminal and destination are the same for cars and passengers in both scenarios. The center of the city measures 2km by 2km = 4km2. The results are displayed in the table below.
In the ideal estimation 作业代做
The distance covered and the time spends on each trip are similar in normal conditions and ideal situation when the number of cars is low. The scenario changes when the number of car increases. Therefore, the time and cost of commuting can be compared between the ideal and normal circumstances. The time spent and distance covered in each trip at normal situation increase by 6.6 and 8.4 percent respectively when the number of cars increases from 300 to 500. Similarly, when the cars are taken to be 1000, the amount of time and distance covered increases. The performance increases when the number of drivers car-pooling is higher than the number of clients waiting to be served.
| N | Number of cars | Users | Users Served | User not Served | Ideal Distance | Ideal Time | Normal Distance | Normal Time |
| 1 | 100 | 40 | 8 | 32 | 117.7 | 271.75 | 119.2 | 278.38 |
| 2 | 100 | 100 | 16 | 84 | 252.58 | 545.50 | 256.63 | 562.19 |
| 3 | 200 | 40 | 18 | 22 | 124.38 | 284.83 | 124.50 | 291.11 |
| 4 | 200 | 100 | 26 | 74 | 175.09 | 389.69 | 180.39 | 408.35 |
| 5 | 300 | 40 | 18 | 22 | 144.9 | 339.40 | 145.68 | 344.61 |
| 6 | 300 | 80 | 38 | 42 | 197.67 | 480.29 | 197.73 | 480.30 |
| 7 | 300 | 150 | 48 | 102 | 180.90 | 428.35 | 182.56 | 432.12 |
| 8 | 300 | 300 | 86 | 214 | 151.68 | 341.91 | 153.93 | 356.92 |
| 9 | 500 | 100 | 49 | 51 | 152.73 | 355.39 | 178.08 | 399.48 |
| 10 | 500 | 250 | 106 | 144 | 199.48 | 445.77 | 200.23 | 473.44 |
| 11 | 500 | 400 | 150 | 250 | 205.22 | 458.79 | 209.22 | 489.85 |
| 12 | 500 | 500 | 184 | 316 | 205.39 | 450.22 | 221.05 | 487.98 |
| 13 | 1000 | 200 | 110 | 90 | 181.23 | 428.89 | 191.74 | 573.78 |
| 14 | 1000 | 500 | 236 | 264 | 201.62 | 469.61 | 217.74 | 654.07 |
| 15 | 1000 | 1000 | 391 | 609 | 210.56 | 471.08 | 220.01 | 675.45 |
Conclusion Carpooling代写
The simulation shows a dynamic carpooling system that can be used to optimally utilize the transport system available as people share rides and costs of commuting. The simulation was developed using Netlogo to study the most efficient and convenient method of commuting in the city of Dublin.
The simulation shows that users have the advantage of car-pooling over other methods of commuting like personal cars. These are economic advantages like lowers cost of commuting, save on time, more distance covered in less time. The simulation offers a solution to the problem of traffic jams, time spent, and distance covered during commuting. As a result, the model is ideal to be used by highly populated areas like cities where numerous traffics jam to reduce the number of cars in the city, and hence the time and cost spend in commuting.
References Carpooling代写

Shaheen, S.A., Chan, N.D., and Gaynor, T., 2016. Casual carpooling in the San Francisco Bay Area: Understanding user characteristics, behaviors, and motivations. Transport Policy, 51, pp.165-173.
Tahmasseby, S., Kattan, L., and Barbour, B., 2016. The propensity to participate in a peer‐to‐peer social‐network‐based carpooling system. Journal of Advanced Transportation, 50(2), pp.240-254.
Wilensky, U., 1999. Center for connected learning and computer-based modeling. In NetLogo. Northwestern University.



