MATH96014 Mathematical Finance
数学金融代写 Consider the probability space Ω = {ω1, ω2, ω3}, with the probability P such that P({ω}) = 1/3 for every ω ∈ Ω. Defifine the random variables
Question 1
(Total: 20 marks)
Consider the probability space Ω = {ω1, ω2, ω3}, with the probability P such that P({ω}) = 1/3 for every ω ∈ Ω. Defifine the random variables
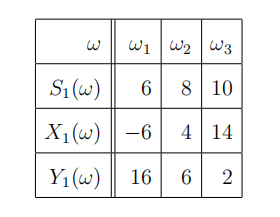
Consider the one-period trinomial model of the market (B, S) made of a bond B with initial price 1 (all prices in a fifixed currency, say £), and interest rate r = 1, a stock whose initial price is S0 = 4, and whose fifinal price is S1. Answer the following questions about the two illiquid derivatives with payoffffs X1, Y1 in the market (B, S).
(a) Is this model free of arbitrage? (3 marks)
(b) Is X1 replicable? (2 marks)
(c) Is Y1 replicable ? (2 marks)
(d) What is the set of arbitrage-free prices of X1? (4 marks)
(e)What is the set of arbitrage-free prices of Y1? (4 marks)
(f) Consider now a derivative with payoffff Z1 which is not replicable in the (B, S) market. Now enlarge the (B, S) market, by assuming that Y is traded at the arbitrage-free price Y0 at time 0. Is the set of arbitrage-free prices of Z1 in the market (B, S, Y ) a singleton? Explain your reasoning. (5 marks)
Question 2 数学金融代写
(Total: 20 marks)
Suppose a British investor can:
- deposit £ in a bank at the (domestic) interest rate r = 1/2
- buy or sell $ (by paying/getting paid in £) at any time n with exchange rate Sn
- deposit $ in a bank at the (foreign) interest rate f
The exchange rate Sn is defifined as the number of units of £ needed to buy one unit of $ at time n, and is assumed to follow the one period binomial model with S0 = 2, u = 2, d = 1/2. Answer the following questions and justify carefully your answers.
(a) Explain why the formula (3 marks)

(d) Consider a forward contract on the exchange rate. In other words, consider the agreement which has no initial cost, and which states that its buyer will buy one $ at the price P0 (called the forward exchange rate) at time 1, where the constant P0 is determined by asking that the arbitrage-free price F0 of the forward contract is zero. What is the value of P0? (5 marks)
(e) What is the replicating strategy h of a call option (on the exchange rate) with strike price 2? (4 marks)
Question 3 数学金融代写
(Total: 20 marks)

Question 4 数学金融代写
(Total: 20 marks)
I bought at time 0 a derivative which gives me the right to purchase, at price c1 > 0 and time t1 > 0, a call option (on an underlying stock S) with expiration t2 > t1 and strike price K2. Assume that the stock price S = (St)0≤t≤t2 follows the Black-Scholes model, and denote with c(x, τ, K) the price at time t of a call option on S with expiry T := t + τ > t and strike K > 0, if St = x (it can be proved that c does not depend on t, it only depends on τ ). Answer the following questions and justify carefully with either proofs or counterexamples.
(a) Prove that, for any value of (τ, K), the function x 7→ c(x, τ, K) ∈ R is strictly increasing for x ∈ (0,∞). Compute its limits as x ↓ 0 and as x ↑ ∞. (3 marks)
(b) Write an equation whose solution is the value of b1 > 0 such that at time t1 if St1 > b1 I should exercise the derivative, if St1 < b1 I should not exercise it, and if St1 = b1 it is irrelevant what I do. Prove that such equation admits one and only one solution. Warning: do not try to solve the equation: it is transcendental, and so it does not have a closed-form analytic solution. (4 marks)
(c) Write a formula, which involves the price c1 and the pricing function c, for the value of the derivative at time t1. (3 marks)
(d) Write down a formula for the function f = f(x, y) such that f(St1 , St2 ) is the payoffff of the option at time t2. (5 marks)
(e) Consider a derivative G on S with payoffff Gt2 = g(St1 , St2 ) at time t2, for some function g = g(x, y). Obtain an explicit formula for the price G0 at time 0 of the derivative G; this formula must be of the form (5 marks)
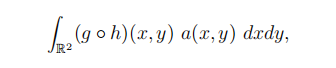
where h, a are functions which you have to determine; explain your reasoning.




