PPHA 44330: Energy and Environmental Economics II
Problem set #1
环境经济学代写 Discrete time resource dynamics: mine deepening. Consider the following problem of a miner facing a constant price…
1.Discrete time resource dynamics: mine deepening. Consider the following problem of a miner facing a constant price p over a finite horizon (T periods). At the start of period 1, the depth of the mine is x1 = X > 0. Denote wt as the vertical feet mined in period t. Denote the amount extracted and sold as qt. Denote the reserves at the beginning of period t as rt, and denote the reserves at the start of period 1 as r1 = R > 0.
Reserves are depleted in period t by extraction in period t but may be augmented by additions to reserves that are caused by making the mine deeper. Let xt denote the total depth of the mine at the start of period t. New additions to reserves in period t are a function f(wt, xt) that is strictly increasing in feet mined wt (though with diminishing returns) and strictly decreasing in feet mined in prior periods. That is, fw > 0, fww < 0, fx < 0, fxx < 0, and fwx < 0. Also, f(0, xt) = 0.
Denote the total cost of deepening the mine as k(wt), which is strictly increasing and strictly convex. Finally, denote the cost of extraction in each period as c(qt, rt), where cq > 0, cqq > 0, cr < 0, crr > 0, and cqr < 0. Thus, increasing reserves has the benefit of lowering extraction costs.
The miner’s discount factor is δ. The miner’s problem is therefore: 环境经济学代写
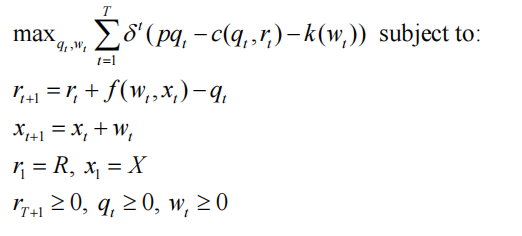
(a) What are the state variables for this problem? What are the controls?
(b) Write down the Lagrangian for this problem (use the short form here and for the rest of the problem set). Think carefully about the direction in which the xt+1 = xt + wt constraint binds (is more depth good or bad for the miner?). Write the Kuhn-Tucker conditions.
(c) Focus on the condition determining wt, the optimal number of feet to deepen the mine in period t. Interpret this equation in terms of the costs and benefits of digging deeper. 环境经济学代写
(d) You should find that both co-state variables are decreasing over time (both in present value). Explain why this is the case.
2. More discrete time resource dynamics: well drilling. Assume the world oil price P is unchanging. Extractors are identical. Each decides when to rent a drilling rig to drill his well. Drilling takes one period, and underground pressure propels X units of oil to the surface in the following period. In each successive period, a drilled well produces (0,1) less oil than in the previous period; the extractor has no control of oil flow and incurs no cost of extracting the oil once the well is drilled. Drilling, however, is costly. There are a finite number of wells to drill, denoted W. The number of undrilled wells remaining at the start of period t is denoted wt. (Note that this set up is similar to that in Anderson, Kellogg, and Salant (2014), though in that paper extractors can reduce oil flow below the capacity constraint.) 环境经济学代写
All rigs rent in the same period for the same rental price. To drill a well, one rig is needed for one period. Denote the number of wells drilled (and therefore rigs rented) at time t as at and the rent required to attract at rigs to the wells as R(at). R(at) is strictly upward-sloping, since using more rigs in a period requires activating less-efficient rigs, hiring part-time workers, and/or attracting rigs from far away.
Assume that extractors take the constant oil price as given and the time path of rig rentals {Rt} as given. Assume the rig rental market clears in every period. Assume all agents discount future costs and earnings at the real interest rate r. Denote the discount factor (1 + r)-1 by δ. Finally, do not require at, W, or wt to be integers.
(a) If an extractor rents a rig in the current period to drill his well, show that his gross revenues over infinite time, discounted to the current period, are given by PXδ(1-δ(1-λ))-1 环境经济学代写
(b) Explain why in equilibrium drilling must cease in finite time (even if the time horizon is infinite), but, prior to that, each extractor must be indifferent about the period when he rents drilling equipment to open his well. That is, if we let γt denote the discounted (to time t = 0) net profit from drilling a well in period t, then γt must be constant.
(c) Explain why in equilibrium both the number of drilling rigs rented and their rental rate decrease monotonically over time.
(d) Let Ft denote the amount of oil flowing from all opened wells at time t. The initial flowrate at time t = 0 is F0 = 0. Since wells drilled in period t do not start producing until period t + 1, we have Ft+1 = Ft(1 – λ) + atX for t > 0. Explain why, in this model, it is possible for aggregate oil flows to increase over time initially (not just from t = 0 to t = 1, but also from t = 1 to t = 2). Would this also be possible if R(at) were constant rather than upward sloping? Why must aggregate oil flows eventually decline toward zero?
(e) Consider formally the extractors’ finite-time version of the problem discussed above:1
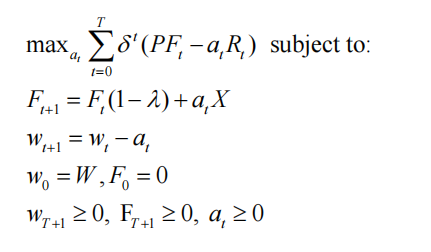
Write all the Kuhn-Tucker necessary conditions for this problem. Let γt denote the co state variable associated with wt, and let θt denote the co-state variable associated with Ft. 环境经济学代写
(f) Interpret the FOC that determines the number of wells to drill in each period. Relate this answer to your answers to (b) and (c) above. What is the interpretation of θt?
(g) Prove that the aggregate wealth of the extractors, discounted to t = 0, is γW.
(h) Prove that θT = 0. Why? Use this and the difference equation governing (θt – θt-1) to derive an expression for θt in terms of P, δ, λ, and T. Compute lim θt. Relate your answer to that for part (a).
3. Hotelling under monopoly, continuous time. (Stiglitz 1976). Consider the simplest version of the Hotelling model discussed in class. There is an initial fixed resource stock S, and extraction is costless. The time horizon is infinite. As in class, let yt denote extraction at time t, and let xt denote the stock of oil remaining at t. Consumption utility u(yt) has u’ > 0 and u” < 0. In class, we showed that in the planner’s problem / competitive equilibrium for this model (without common pool externalities), price must rise at the rate of interest r until p = u’(0), at which point extraction stops (and extraction declines asymptotically to zero if u’ is unbounded).
(a) Suppose the entire stock is controlled by a monopolist. Write down the monopolist’s problem and the necessary conditions for an optimum. Interpret these conditions; what does the monopolist want to do to maximize profits?
(b) Suppose that demand is constant elasticity. How does the monopolist’s optimal extraction path compare to that in the competitive equilibrium? How do prices compare? (note: you can do this qualitatively; you don’t need to solve for the exact path as a function of S, r, and the utility function parameters) 环境经济学代写
(c) Now suppose that demand is linear. How does the monopolist’s optimal extraction path compare to that in the competitive equilibrium? How do prices compare? (note: you can do this qualitatively; you don’t need to solve for the exact path as a function of S, r, and the utility function parameters. That said, you may find it useful to compare the equations that determine the optimal stopping time under competition and monopoly.)
(d) Explain any difference between your answers to (b) and (c).4. Uranium production, continuous time. This problem considers production of uranium, an exhaustible resource. The initial stock of uranium is given by R0 > 0, and let yt denote the rate of uranium extraction in each period t (time is continuous). The utility from uranium consumption is given by u(yt), with u’(∙) > 0 and u’’(∙) < 0. u’(0) is finite (in other words, there is a “choke price” u’(0) above which consumers do not demand uranium). The extraction cost is given by c(yt), with c(0) = 0, c’(∙) > 0, c’(0) < u’(0), and c’’(∙) > 0. Let Rt denote the stock remaining at t.

The time horizon is infinite (and time begins with t = 0) and the social discount rate is ρ. Throughout the problem, assume that uranium cannot be stored above ground.
(a) Write down the social planner’s problem for maximizing the value of the resource. Write down the planner’s current value Hamiltonian.
(b) Write down the first order necessary conditions for this problem. 环境经济学代写
(c) On a graph, sketch the time paths of extraction yt, the resource price u’(yt), and the shadow value of stock μt (in current value), starting from t = 0 and continuing until the uranium resource is exhausted. Explain why extraction must cease at some finite time T.
(d) Now suppose that at some time t* < T, there is an unexpected increase in resource demand, so that the new marginal utility function is given by v’(yt) = u’(yt) + α, where α >0 On a graph, sketch the time paths of extraction yt, the resource price u’(yt), and the shadow value of stock μt (in current value), starting from t = 0 and continuing until the uranium resource is exhausted. Discuss the intuition behind the behavior of these variables at t*.
(e) Now suppose that the demand shock discussed in part (d) was anticipated in advance. Specifically, suppose that it was known at t = 0 that the demand shock would occur at time t* . 环境经济学代写
On a graph, sketch the time paths of extraction yt, the resource price u’(yt), and the shadow value of stock μt (in current value), starting from t = 0 and continuing until the uranium resource is exhausted. Discuss how these paths are similar or different to what you found in part (d), including whether the starting values y0, u’(y0), and μ0 are larger or smaller than in part (d).
(f) Now suppose that investments in production capacity are required to mine the uranium. Specifically, at all times t production must be less than the installed capacity Kt, so that we have the constraint yt ≤ Kt. Capacity can be increased through investment at rate at, so that ? ? = ?? . Investment costs are given by f(at), where f(0) = 0, f’(∙) ≥ 0, f’(0) = 0, and f’’(∙) > 0. The initial capacity K0 equals 0. Capacity does not depreciate once it is built. Write down the planner’s current value Hamiltonian for this problem. Let θt denote the co-state variable on capacity, and let φt denote the Lagrange multiplier on the capacity constraint.
(g) Write down the first order conditions necessary for maximization. 环境经济学代写
(h) Prove that in the limit as t goes to infinity, θt goes to zero. Intuitively, why is this the case?
(i) On a graph (or several graphs to reduce clutter), sketch the time paths of extraction yt, capacity Kt, the resource price u’(yt), and the shadow value of stock μt (in current value), starting from t = 0 and continuing until the uranium resource is exhausted.
5. Storage and uncertainty. Suppose that, following the events depicted in the (awful) movie Avatar, the world has a fixed stockpile S of the substance “unobtanium”. This stockpile is divided across a large number of firms, all of which act as price takers. Mining additional unobtanium is not possible, since humans have been kicked off the planet Pandora from which unobtanium was mined. The cost of storage is zero. 环境经济学代写
The total demand for unobtanium is given by the downward-sloping function P(Q), where Q is the total amount withdrawn from the stockpile. At a future and known time T, it is certain an asteroid made of 100% unobtanium will impact earth, making all unobtanium stockpiles worthless. Between today (t = 0) and T, there is a constant hazard α > 0 that a substitute to unobtanium will be discovered, which would also make all unobtanium stockpiles worthless. Thus, the probability the unobtanium is valued by consumers for times t < T is given by e-αt .
The firms owning the stockpile all have the same discount rate, r. Time is continuous. Let st denote the amount of the stockpile remaining at any time t.
(a) Write down the resource owners’ current value Hamiltonian and first order conditions.
(b) Suppose that no substitute for unobtanium is discovered before T (the probability of this happening is e-αT). Describe the equilibrium price path, and draw it on a graph. 环境经济学代写
(c) On the same graph, draw the expected price path starting from t = 0 (i.e., from the perspective of firms at t = 0, what is the expected price at all future times, given that the price will fall to zero in the event of the discovery of a substitute?). Explain your answer.
(d) On the same graph, draw the equilibrium price path for unobtanium in a counterfactual world in which there are no possible substitute technologies (equivalently, α = 0). Explain difference between this line and the lines you drew for parts (b) and (c).




