Homework 3
算数函数代写 You’ve already seen ϕ(n), the number of integers between 1 and n coprime to n. Here are three other “arithmetic” functions:
1 Arithmetic Functions – Basics
You’ve already seen ϕ(n), the number of integers between 1 and n coprime to n. Here are three other “arithmetic” functions:
❼ σ(n), the sum of all the positive divisors of n (including n itself), 算数函数代写
❼ τ (n), the number of positive divisors of n, and
❼ µ(n), which is 0 if n is divisible by a square other than 1 and µ(n) = (−1)k if n = p1p2 · · · pk, the product of k distinct primes.
An arithmetic function f : N → C is called multiplicative if f(ab) = f(a)f(b) for all a and b that are relatively prime. It is called totally multiplicative if f(ab) = f(a)f(b) for all a and b.
Problem 1. 算数函数代写
(a) Come up with (and prove!) a closed formula for σ(n) and τ (n) in terms of the prime factorization of n (similar to, if ![]()
![]()
(b) Show that σ(n)ϕ(n) < n2 for n ≥ 2.1

(c) Show that all of ϕ, σ, τ , and µ are multiplicative. Which ones are totally multiplicative?
Problem 2. If f and g are arithmetic functions, defifine 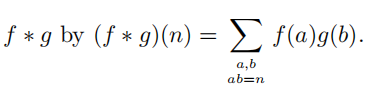
(a) Show that f ∗ g = g ∗ f and (f ∗ g) ∗ h = f ∗ (g ∗ h). 算数函数代写
(b) Find an arithmetic function id such that id ∗ f = f for all f.
(c) When can you fifind “∗-inverses (i.e. f and g are ∗-inverses iffff f ∗ g = id)?




