CS 535 Homework 2
算法分析作业代写 1. Let G = (U; W; E) be a bipartite graph. Show that for any S; T ⊆ U, |N (S)| + |N (T)| ≥|N (S∩T)|+|N (S∪T)| .
1. Let G = (U; W; E) be a bipartite graph. Show that for any S; T ⊆ U, 算法分析作业代写
|N (S)| + |N (T)| ≥|N (S∩T)|+|N (S∪T)| .
2. Let G = (U; W; E) be a bipartite graph. Let I denote the collection of subsets of U which can be covered by some matching of G. Suppose that S,T ∈ I and |S|< |T|. Show that there exists v ∈ T \ S such that S ∪{v}∈I.
3. Let G = (U; W; E) be a bipartite graph. Given a maximum matching M of G, describe a linear -time algorithm to compute a set T ⊆ U satisfying that
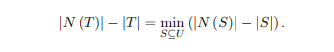
(Hint: For each S ⊆ U, (U n S) [ N (S) is a vertex cover of G.) 算法分析作业代写
4. Let G = (U; W; E; w) be an edge-weighted bipartite graph with jUj = jV j. Suppose that the edge weight function w satisÖes that for w (e) 0 each e 2 E and the total weight of the edges incident to each vertex v 2 U [ W is exactly one. Show that G has a perfect matching.
(Hint: Use the Hallís condition.)

(a) Show that D has a negative circuit if and only if G has a perfect matching with negative weight.




