Exam II

Exam代写 When asked for time or space requirements, use Big-O notation, and use ‘n’ for the number of items in the collection or arrays.
Name: ___________________
Comp 271: Data Structures, Fall 2017 Exam代写
21.4 points possible (0.4 pts/ question unless noted)
10 pages, 1 hr 35 min time (~10 mins / page). Please pace appropriately.
When asked for time or space requirements, use Big-O notation, and use ‘n’ for the number of items in the collection or array
IMPORTANT NOTE: for numbered problems, if you answer and receive no partial credit, you will be deducted up to an additional 0.4 pts.
In the Sorts homework we used ArrayList to perform array-like operations. ArrayList uses methods to do the same things we did with indexed arrays.
Examples: myArr[k] = myArr[k+1]; myArr.set(k, myArr.get(k+1) ); int [] myArr = new int[50]; ArrayList<Integer> myArr = new ArrayList<Integer>(50)
1. Translate the following line for when myArr is an ArrayList. Yes, it makes no sense.
myArr[temp] += myArr[myArr[k]];
2. In the list above, pick one of the Big-O functions above for the situations below: Exam代写
a) The time for the fastest sort for a shuffled, random array
b) The number of times you can subtract 100 from the number ‘n’ before it hits 0
d) The number of times you can multiply a number ‘n’ by 0.9 before it reaches 1
e) The speed of finding a value in an array, given the index
An important highlighted change is bolded and underlined in the code
public static int recFunc (int n, int count) {
if (n > 1) {
return (recFunc (n - 10, count + 1) );
} else {
return (count);
}
}
1. What value does recFunc(100,0) return, exactly. Exam代写
2. Approximately what mathematical function of ‘n’ does recFunc returns with large ‘n’ and ‘count’ at 0. (hint: use your answer to #1 to help think about it)
3. How much time, in Big O notation, does recFunc take?
4. For each recursive call, O(1) memory must be placed on the recursive function stack. In Big-O notation, how much additional memory is necessary to compute the solution for a value ‘n’?
Provide the Big O time complexity for each function below of the following basic data structures
1. HashMap (the standard map/dictionary implementation)
a)_____ Find by key (assuming well implemented with minimal collisions)
b)_____ Find by value
c)_____ Insert (worst case, you have to resize the array used to implement it)
2. Linked list
a)_____ Find by index
b)_____ Find the first value in the list
c)_____ Insert given a random index
d)_____ Insert when given a pointer to the node location
3. Array (or ArrayList)
a)_____ Find by index
b)_____ Find by value (unsorted)
c)_____ Find by value (sorted, searching intelligently)
d)_____ Insert at a random index location
4. True / False: PriorityQueue implements a priority queue in the java collections framework using an AVL tree, which is one of the most common ways a priority queue is implemented.
1. Fill the following table with the big-O time of each operation (2.0 pts, -0.4 per mistake, no added penalty) Exam代写
| Add(element) | Remove(element) | Contains(element) | |
| LinkedList (doubly-linked) | |||
| Heap (priority queue) | root only: ________ | ||
| Skip list (expected) | |||
| TreeSet/TreeMap with an AVL tree (a balanced binary search tree) | |||
| ArrayList (Unsorted array) | No empty spaces: | ||
| Sorted array | No empty spaces: | ||
| HashSet/HashMap | With resizing: | No resizing: | By key: _______By value: ______ |
LinkedList Exam代写
The following questions involve a doubly-linked list. For reference, the DoublyLinkedNode class used in the linked list implements the following functions:
public DoublyLinkedNode<E> previous(); public void setPrevious(DoublyLinkedNode<E>) public DoublyLinkedNode<E> next(); public void setNext(DoublyLinkedNode<E>); public E value(); public void setValue(E);
There are some mistakes in the code for the remove function for this doubly-linked list, which iterates through the list using ‘finger’ and removes the item with the same value as the passed object, returning the object removed. The mistakes are in bold and underlined below. Replace the parts that are wrong with the correct code.
(6 fixes total – 0.4 pts each, no added penalty)
public E remove(E value) {
// post: first element matching value is removed from list
DoublyLinkedNode<E> finger = null;
// iterate to the item to be removed
while (finger == null && !finger.value().equals(value)) {
finger = finger.next();
}
if (finger != null) {
// remove the node and return the element in it
// fix the next pointer of the node to the left
if (finger != null) {
finger.previous().setNext(finger.next());
} else {
head = finger.next();
}
// fix the previous pointer of the node to the right
if (finger.previous() != null) {
finger.next().setPrevious(finger.previous());
} else {
tail = finger;
}
count++; // fewer elements
return finger.value();
}
// if finger is null
return null;
}
Stacks & Queues Exam代写
1. Match the following implementations with the facts about them. The matching should be one-to-one (one and only one for each) (1.2 pts, -0.4 pts/mistake)
The five queue implementations:
A) a singly-linked list with no tail pointer
B) a doubly-linked list
C) a circularly-linked list (tail node points to the head, and you maintain a tail pointer)
D) an array, adding and removing from the end only
E) an circular array – having the head move (not just at index 0) during add or removes from the head
Facts about those implementations: Exam代写
______ Great FIFO and LIFO, O(1), but you have to deal with capacity vs. size issues
______ Great FIFO and LIFO, O(1), no capacity issues and you can remove either from the head or tail.
______ O(1) for both add and remove as a FIFO and LIFO queue, but you can only remove from the head for that speed.
______ Great LIFO, terrible FIFO (that is, O(n)). ArrayList essentially implements it for you (using add(E) and remove(myList.size()-1) )
______ Great LIFO, terrible FIFO (that is, O(n)) as normally implemented. Elements are not in contiguous portions of memory.
2. If we take a typical singly-linked list implementation and maintain a pointer to the tail, which of the following are O(1) operations.
Circle all the apply. (0.6 pts, -0.2 per mistake)
a) Removing the tail element Exam代写
b) Removing the second element (the one the head points to)
c) Adding an element at the head
d) Adding an element to the tail
e) Removing the head element
f) Removing the second to last element (the one that points to the tail element)
Start fresh with the following heap for the next two problems. Note, no partial credit will be given for incorrect answers, but there will also be no added penalty.
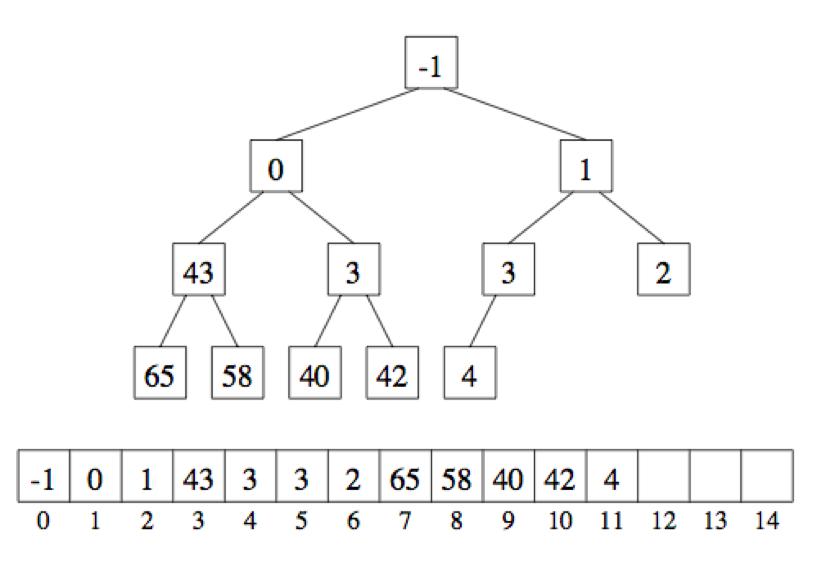
1. Write the resulting heap in tree form upon removing the TWO highest priority/lowest value elements. (Hint: replace the root with the last value in the heap, and percolate that value down to satisfy the heap property – no need to show work). (0.6 pts)
2. Starting with the original heap again (before doing the problem before), write the resulting heap if you add the values 0 and 1 to it (hint: add at the end and percolate up – no need to show work) (0.6 pts)
4 Oh, no! someone forgot which index equations match which relationships. Match them. Write parent, left child, and right child next to the appropriate equation. Hint: use the example above to check them.
a) 2*index + 1
b) 2 * (index + 1)
c) (index-1) / 2
Hash Tables
Suppose you have a class called ‘Student’ which holds student information and uses the student’s ID as the key.
Here is the hashCode method for this class – NOTE THE VALUE ‘7’:
public int hashCode(){
return (7 * this.ID);
}
1. Hash the following student ID/names pairs into the following hash table, which uses LINEAR PROBING to deal with collisions. Use the remainder of the hashCode divided by 5 to determine the index. (1.6 pts, -0.4 per mistake, no added penalty)
ID NAME
1 Mary
11 Sarah
3 Kat
6 Matt
Index <key, name>
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 |
2. For a singly-linked list with a tail pointer…
a) which end(s) can you add to if you will use it as a FIFO queue?
b) which end(s) can you add to if you will use it as a LIFO queue?
1. Write the letter for the following data structures next to the description. Note, the matching is one-to-one so if one appears suitable to multiple descriptions it may have to change so the others match.
(2.0 pts total, -0.3 for each wrong, no additional penalty)
___ If there are O(n log n) evenly distributed edges, search for an edge is O(log n)
___ The fastest, best implementation to represent a dense graph
___ This type of graph is useful for showing dependencies between methods
___ Use this to represent relationships with different strengths between items
a) weighted b) directed c) adjacency matrix graph d) linked-list graph
___ Primitives
___ Wrapper object classes
e) Integer, Double f) int, double
___ O(1) search with index, O(log n) fastest search for a value, does not resize easily
___ O(1) search with index, O(n) fastest search for a value, does not resize
___ O(1) search with index, O(n) fastest search for value, dynamically resizes
___ Great LIFO, bad FIFO queue unless you add a tail pointer and add at the tail
___ A Deque – great LIFO and FIFO behavior since the head and tail are symmetric
g) ArrayList h) singly-linked list Exam代写
j) LinkedList k) sorted array l) unsorted array
___ No extra methods in this, only a promise that duplicates are not allowed
___ You can only access elements on the top or bottom of this interface
___ This isn’t a sub-interface of java.util.Collection since it only stores associations
___ The super-interface for most interfaces in the Java collections framework
___ A group of static methods that work on collections (e.g. shuffle, sort, …)
___ You can access elements by an index, but speeds can range from O(1) to O(n)
m) Map n) Queue o) List p) Set q) Collection r) Collections
___ this tree is self-balancing for fast, efficient behavior
___ an in-order traversal of this tree gives the elements in sorted order
___ this has no particular ordering. e.g. heaps are abstractly represented as these.
s) binary tree t) binary search tree u) AVL tree
___ an alternative to hash tables that maintains items in sorted order
___ a map implementation which is O(1) and fastest for very small load factors
___ a map which can hold more items than its underlying array
___ useful when all you need to do is choose the highest/lowest value each time
___ same expected times as a AVL tree for add/search/remove operations
v) treemap w) hash table, chaining x) hash table, linear probing
y) skip list z) heap/priority queue
Assuming all the functions in our SkipList were implemented with reasonable efficiency. What is the Big O for each of the following functions. Assume our skiplist has ‘n’ elements, and any passed collection also has ‘n’ elements. Note, the questions below are numbered so being wrong incurs an added penalty. You will not receive less than a 0 for this page. (0.4 pts / question, 5.6 pts total, note the penalty applies here to each questions separately).

更多其他:prensentation代写 Case study代写 心理学论文代写 哲学论文代写 计算机论文代写 毕业论文代写 论文代写




您必须登录才能发表评论。