autocorrelation functions代写 Exercise Set代写 Finance代写

c UNFVKRSFTY OF YORK

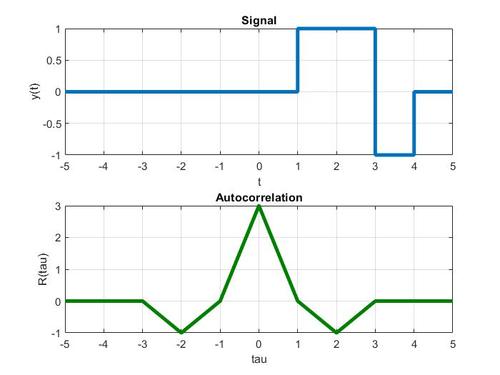
autocorrelation functions代写 What type of stylised facts can you observe by comparing the correlograms for stationary and nonstationary processes.

 

Assessed Coursework for the Degree of MSc at DERS ECO00041 Time Series Exercise Set 1 (10%) Autumn 2019

1. (a) Are the following stochastic processes covariance-stationary?autocorrelation functions代写

(ⅰ)y_t = 0.9y_t—1 ‡ o_t,  o_t ~ ⅱdN .0, o^XΣ

(ⅱ) y_t =    o_1t ‡ ,to_Xt,  o_fit ~ ⅱdN .0, o^X Σ ,

o_Xt ~    ⅱdN .0, o^X Σ ,  E (o_1to_Xt) = 0 ƒ ov a11 t, s

(ⅲ) y_t = y_t—fi — 0.16y_t—X ‡ o_t,  o_t ~ ⅱdN .0, o^XΣ

(b) Derive their autocorrelation and partial autocorrelation functions and comment on the results.

2. (a) Consider the stationary AR(fi) process,

y_t = $y_t—1 ‡ o_t,  o_t ~ ⅱdN .0, o^XΣ ,autocorrelation functions代写

and derive autocorrelation functions given by

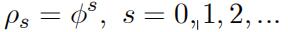
Draw the correlograms for $ = (0.8, 0.†, 0.£} and comment on the results.

(b)Show that random walk process,

y_t = $y_t—1 ‡ o_t,  ƒ ov t > 0,  y_O = 0,  o_t ~ⅱdN （0, o^XΣ）

does not satisfy the stationarity condition. Next, show that the ACF‘s for the random walk process is given by

g = t — s , s = 0, 1, 2, …

(c)What type of stylised facts can you observe by comparing the correlograms for stationary and nonstationary processes. Describe a few reasons that it is important to distinguish between the difference- stationary and the trend-stationary process.

3.Consider the AR(fi) regression with an intercept:

y_t = α ‡ $y_t—fi ‡ o_t, t =1, …, T,

where y_t is a scalar variable, α and $ are unknown parameters, and

o_t ~ ⅱdN 0, o^X . We assume that the initial value y_O is fixed.

(a)Derive the OLS estimator of $ and its asymptotic distribution when |$| c fi.

(b)Explain how to test H0 : = 0 against H1 : = 0

|$_O| c fi.autocorrelation functions代写

(c)Describe how to test H_O : $ = fi against H_fi : $ c fi.

(d)Suppose that o_t is now serially correlated as

o_t = go_t—fi ‡ u_t,

where u_t ~ ssdN  0, o^X . Discuss if the testing procedures derived in

(b) and (c) are still valid. If not, explain how to do a valid inference.

4.(a) Consider the AR(fi) process,

y_t = α ‡ $y_t—1 ‡ u_t, t = 1, …, T,

where u_t ~ⅱd .0, o^XΣ. Let

y_T ‡h : unknown value of y in future period T ‡ h, h = 1, 2, …

yT ‡h: forecast of y

T ‡hmade on the basis of information available at time T,

e_T ‡h = y_T ‡h — y_T ‡h : forecast error.

Then, show that as h ‹ œ ^

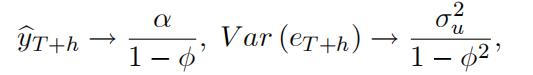
and comment on these results.

(b) Suppose that $ = fi. Then what do you get for y_T ‡h

and V av (e_T ‡h)as h ‹ œ? Comment on your findings.

5. A research uses a sample of £00 observations on y_t, autocorrelation functions代写

the number (in fi000s) of unemployed persons, to model the time series behavior of

the series and to generate predictions. First, she computes the sample autocorrelation functions with the following results:

g^s	1	2	3	4	5	6	7	8	9	10
s	0.83	0.71	0.6	0.45	0.44	0.35	0.29	0.2	0.11	-0.01

(a)What do you mean by the sample autocorrelation functions? Does the above pattern indicate that an AR or an MA representation is more appropriate? Why?autocorrelation functions代写

Next, the sample partial autocorrelation functions are obtained as:

s	1	2	3	4	5	6	7	8	9	10
SP ACFs	0.83	0.16	-0.09	0.05	0.04	-0.05	0.01	0.1	-0.03	-0.01

What do you mean by the sample partial autocorrelation func- tions? Why is the first PACF equal to the first older ACF? Does the above pattern indicate that an AR or an MA representation is more appropriate? Why?

The researcher decides to estimate, as a first attempt, an AR(1) model:

y_t = α ‡ $y_t—1 ‡ o_t

and obtained the estimate, $^1  = 0.83 with a standard error of 0.07.

(c)Which estimation method is appropriate for estimating an AR(1) model? Explain under which conditions it is consistent and efficient.

(d)Perform the test for the null hypothesis, $ = 0.9.

(e)Perform the unit root test based on the above regression results. Next, the researcher extends the model to AR(£) regression with the following results (standard errors in parenthesis):

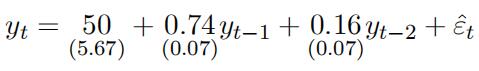
(f)Would you prefer AR(2) model to the AR(1) model? How would you check whether ARMA(2,1) may be more appropriate?

(g)What do the above estimation results tell you about the validity of the unit root test conducted in (e)? Then how would test for a unit root in the AR(£) model?autocorrelation functions代写

(h)Suppose that the last two quarterly unemployment levels for fi996Ø3 and fi996Ø4 were ††0 and 600. Evaluate the predictions for fi99FØfi and fi99FØ£. Can you say anything sensible about the predicted values for £0£3Øfi (and its accuracy)?

6.Consider the following simple relationship between aggregate savings autocorrelation functions代写

S_t and aggregate income Y_t:

S_t = α ‡ ØY_t ‡ o_t, t = 1, …, T.

For some country this relationship is estimated by OLS over the years1956-2005 (T =50). The results are given below:

Variable	Coefficients	Standard error
Constant	38.90	4.57
Y	0.098	0.009

o^ =    ££.57,  R^X = 0.93,  DW  = 0.F0

where o^ is the standard error of regression, R^X is the multiple correla- tion coefficient, and DW is the Durbin-Watson statistic.

(a)How would you interpret the coefficient of 0.098 on income?

(b)Explain why the result indicate that there may be a problem of positive autocorrelation. Can you give arguments why in economic models positive autocorrelation is more likely than negative one?

(c)What are the effects of autocorrelated residuals on the BLUE prop- erty of the OLS estimator?autocorrelation functions代写

Now we assume that both S and Y are nonstationary I(fi) series.

(d)Is there any indication that the relation between them is spurious?

(e)Describe two different tests that can be used to test the null hy- pothesis that S and Y are not cointegrated.

(f)Are there reasons to correct for autocorrelation in errors when we estimate a cointegrating regression?

7.Short essay questions autocorrelation functions代写

(a)The Box and Jenkins three-stage ARMA(p, q) modelling.

(b)Describe and compare the DF test and the KPSS test.

(c)Give an example from Economics or Finance where cointegration among a set of variables may be expected. Explain, by reference to the implication of no-cointegration, why cointegration between the series might be expected. For example, describe a cost of carry model for cash and futures price indexes.

Notes: The first in-course exercise (10%) will be downloadable from VLE on Monday 14 October, and one anonymous copy of this assignment (only with your exam number) must be submitted to the Economics reception

desk no later than 3PM on Wednesday 30 October. Handwritten reports are accepted. Failure to meet this initial deadline will result in a reduc- tion of marks (please see VLE for details). Faxed or emailed copies of the assignment will not be accepted.

更多其他:prensentation代写 Case study代写 文学论文代写 商科论文代写 艺术论文代写 人文代写 Case study代写 心理学论文代写 哲学论文代写

合作平台：天才代写 幽灵代写  写手招聘