英国Matlab代写 AMME5520: Project Part 2代写 cs代写

AMME5520: Project Part 2

英国Matlab代写 The following questions explore control and navigation via the material from weeks 4-9. Submit a report through TurnItIn…

The following questions explore control and navigation via the material from weeks 4-9. Submit a report through TurnItIn justifying the design decisions you have made and exploring their consequences. The report must be thorough but concise (feedback from your tutor will be valuable in achieving the right balance).

All matlab code must also be submitted through TurnItIn. While you are encouraged to discuss approaches with tutors and your fellow students, all code, analysis and submitted writing must be entirely your own work.

Problem Specification 英国Matlab代写

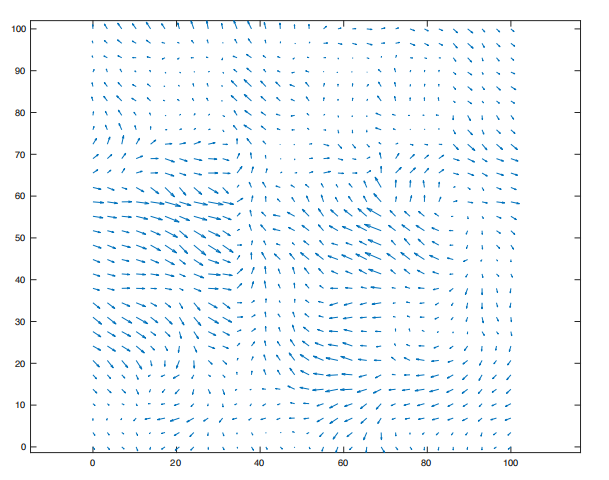
This problem continues from Part 1, in which motions were planned through a wind field similar to the one below.

In this part, consider that the unmanned vehicle is a small hovercraft, with dynamics

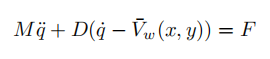where 英国Matlab代写

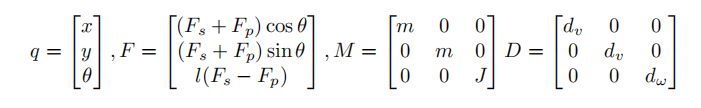
with q  comprising the position (x, y) in metres and angle (θ) in radians, F  the forces and torques, M the mass/inertia matrix, and D the damping matrix, and

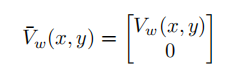
where V_w(x, y) is the wind vector at the point x, y, as in Part 1.

The control inputs are port and starbord thrust F_p, F_s. In nominal forward motion, F_p = F_s = 2 and each has a maximum value of 2.5.

The  parameters  are  mass  m  =  5,  inertial  J   =  0.05,  friction  coefficients

d_v = 4, d_ω = 0.4, and l = 0.1.

Your task is to design a navigation and control system to follow the paths you found in Part 1. : 英国Matlab代写

1. (25 marks) Build a simulink model¹for the above scenario, which simulates the nonlinear dynamics of the hovercraft and the effect of the wind fifield.
2. (10marks) Compute the linearisation of the dynamics along a  Notice that if θ is constant, then the linearisation of the nonlinear dynam- ics is in fact an LTI system. Is it controllable?
3. (20marks) Assuming full state measurement (x, y, θ, x˙, y˙, θ˙), design a control system that controls the vehicle along the paths you found in Part 1.

There are various ways to do this. One simple approach (you don’t have to take this approach) is to use a piecewise linear path , i.e. a sequence of  straight  lines  with  piecewise  constant  θ,  and  design  LTI  controllers  to track each in turn. Is there a better coordinate system than the one above?

4. (10 marks) Design a controller that, if the wind vector is constant (butunknown) along a straight-line segment, keeps the hovercraft exactly on the line segment, while still moving along it.
5. (20 marks) Suppose now that the following measurements are available:(x, y) position via GPS, x¨, y¨ and θ˙  via an inertial measurement unit, and θ from a compass. 英国Matlab代写

The measurements are noisy (assume Gaussian white noise) with variancesAssume also the initial position is estimated with variance Simulate these noisy measurements in your model, and design a Kalman filter to estimate the hovercraft’s true state, and incorporate this into your controller above.

6. (Bonus10 marks) Assume now that GPS has failed, but the bearing to a single known landmark (randomly placed in the map) can be measured, with variance of 0.1 radians². Design an EKF that achieves successful navigation in this scenario.

You can use another simulation methodology if you like, e.g. an ODE solver in another language