CCF 非专业级软件能力认证
CSP-J/S 第二轮认证
计算机技术代写 1. 文件名(程序名和输入输出文件名)必须使用英文小写。 2. C/C++ 中函数 main() 的返回值类型必须是 int,程序正常结束时的返回值必须是 0。3. 提交的程序代码文件的放置位置请参考各省的具体要求。
4. 因违反以上三点而出现的错误或问题…
提高组
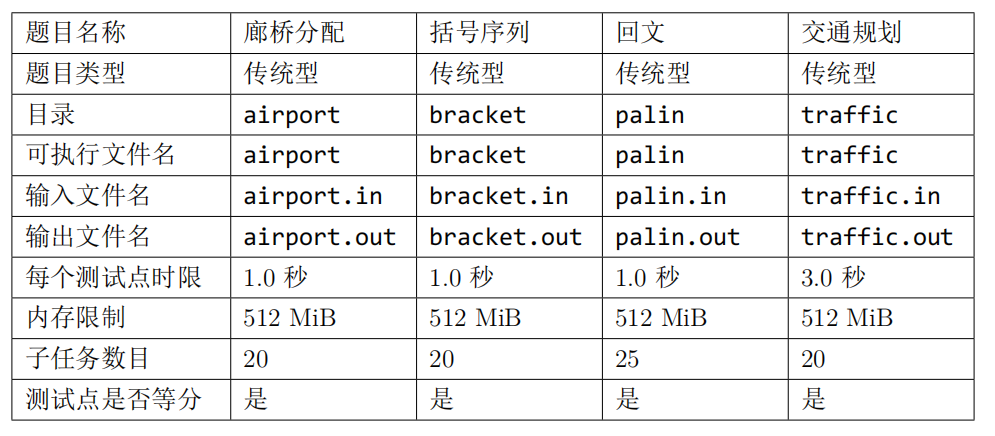
提交源程序文件名

编译选项

注 .意 .事 .项( .请 .仔 .细 .阅 .读)
- 文件名(程序名和输入输出文件名)必须使用英文小写。
- C/C++ 中函数 main() 的返回值类型必须是 int,程序正常结束时的返回值必须是 0。
- 提交的程序代码文件的放置位置请参考各省的具体要求。
- 因违反以上三点而出现的错误或问题,申述时一律不予受理。
- 若无特殊说明,结果的比较方式为全文比较(过滤行末空格及文末回车)。
- 程序可使用的栈空间内存限制与题目的内存限制一致。
- 全国统一评测时采用的机器配置为:Inter(R) Core(TM) i7-8700K CPU @3.70GHz,内存 32GB。上述时限以此配置为准。2021 CCF 非专业级软件能力认证 CSP-J/S 2021 第二轮认证
- 只提供 Linux 格式附加样例文件。
- 评测在当前最新公布的 NOI Linux 下进行,各语言的编译器版本以此为准。
廊桥分配(airport) 计算机技术代写
【题目描述】
当一架飞机抵达机场时,可以停靠在航站楼旁的廊桥,也可以停靠在位于机场边缘的远机位。乘客一般更期待停靠在廊桥,因为这样省去了坐摆渡车前往航站楼的周折。然而,因为廊桥的数量有限,所以这样的愿望不总是能实现。
机场分为国内区和国际区,国内航班飞机只能停靠在国内区,国际航班飞机只能停靠在国际区。一部分廊桥属于国内区,其余的廊桥属于国际区。
L 市新建了一座机场,一共有 n 个廊桥。该机场决定,廊桥的使用遵循“先到先得”的原则,即每架飞机抵达后,如果相应的区(国内/国际)还有空闲的廊桥,就停靠在廊桥,否则停靠在远机位(假设远机位的数量充足)。该机场只有一条跑道,因此不存在两架飞机同时抵达的情况。
现给定未来一段时间飞机的抵达、离开时刻,请你负责将 n 个廊桥分配给国内区和国际区,使停靠廊桥的飞机数量最多。
【输入格式】
从文件 airport.in 中读入数据。
输入的第一行包含 3 个正整数 n, m1, m2 分别表示廊桥的个数、国内航班飞机的数量、国际航班飞机的数量。
接下来 m1 行是国内航班的信息,第 i 行包含 2 个正整数 a1,i, b1,i,分别表示一架国内航班飞机的抵达、离开时刻。
接下来 m2 行是国际航班的信息,第 i 行包含 2 个正整数 a2,i, b2,i,分别表示一架国际航班飞机的抵达、离开时刻。
每行的多个整数由空格分隔。
【输出格式】 计算机技术代写
输出到文件 airport.out 中。
输出一个正整数,表示能够停靠廊桥的飞机数量的最大值。
【样例 1 输入】


【样例 1 输出】

【样例 1 解释】
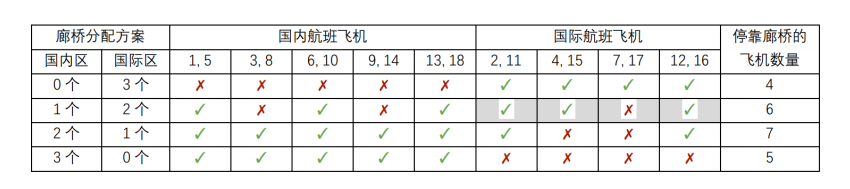
图 1: 样例图片
在图中,我们用抵达、离开时刻的数对来代表一架飞机,如 (1, 5) 表示时刻 1 抵达、时刻 5 离开的飞机;用 √ 表示该飞机停靠在廊桥,用 × 表示该飞机停靠在远机位。
我们以表格中阴影部分的计算方式为例,说明该表的含义。在这一部分中,国际区有 2 个廊桥,4 架国际航班飞机依如下次序抵达:
- 首先 (2, 11) 在时刻 2 抵达,停靠在廊桥
- 然后 (4, 15) 在时刻 4 抵达,停靠在另一个廊桥
- 接着 (7, 17) 在时刻 7 抵达,这时前 2 架飞机都还没离开、都还占用着廊桥,而国际区只有 2 个廊桥,所以只能停靠远机位
- 最后 (12, 16) 在时刻 12 抵达,这时 (2 11) 这架飞机已经离开,所以有 1 个空闲的廊桥,该飞机可以停廊桥
根据表格中的计算结果,当国内区分配 2 个廊桥、国际区分配 1 个廊桥时,停靠廊桥的飞机数量最多,一共 7 架。
【样例 2 输入】 计算机技术代写


【样例 2 输出】

【样例 2 解释】
当国内区分配 2 个廊桥、国际区分配 0 个廊桥时,停靠廊桥的飞机数量最多,一共4 架,即所有的国内航班飞机都能停靠在廊桥。
需要注意的是,本题中廊桥的使用遵循“先到先得”的原则,如果国际区只有 1 个廊桥,那么将被飞机 (1, 19) 占用,而不会被 (3, 4)、(5, 6)、(7, 8)、(9, 10) 这4 架飞机先后使用。
【样例 3】
见选手目录下的 airport/airport3.in 与 airport/airport3.ans。
【数据范围】 计算机技术代写
对于 20% 的数据,1 ≤ n ≤ 100, 1 ≤ m1 + m2 ≤ 100。
对于 40% 的数据,1 ≤ n ≤ 5000, 1 ≤ m1 + m2 ≤ 5000。
对于 100% 的数据,1 ≤ n ≤ 100000, 1 ≤ m1 + m2 ≤ 100000。
所有 a1,i, b1,i, a2,i, b2,i 为数值不超过 108 的互不相同的正整数。
保证 ∀i ∈ [1, n], a1,i < b1,i, a2,i < b2,i。
第 5 页 共 13 页2021 CCF 非专业级软件能力认证 CSP-J/S 2021 第二轮认证
括号序列(bracket)
【题目描述】 计算机技术代写
小 w 在赛场上遇到了这样一个题:一个长度为 n 且符合规范的括号序列,其有些位置已经确定了,有些位置尚未确定,求这样的括号序列一共有多少个。
身经百战的小 w 当然一眼就秒了这题,不仅如此,他还觉得一场正式比赛出这么简单的模板题也太小儿科了,于是他把这题进行了加强之后顺手扔给了小 c。
具体而言,小 w 定义“超级括号序列”是由字符 ( 、)、* 组成的字符串,并且对于某个给定的常数 k ,给出了“符合规范的超级括号序列”的定义如下:
1、() 、(S) 均是符合规范的超级括号序列,其中 S 表示任意一个仅由不 .超 .过 k .个字符 * 组成的非空字符串(以下两条规则中的 S 均为此含义);
2、如果字符串 A 和 B 均为符合规范的超级括号序列,那么字符串 AB 、ASB 均为符合规范的超级括号序列,其中 AB 表示把字符串 A 和字符串 B 拼接在一起形成的字符串;
3、如果字符串 A 为符合规范的超级括号序列,那么字符串 (A) 、(SA) 、(AS) 均为符合规范的超级括号序列。
4、所有符合规范的超级括号序列均可通过上述 3 条规则得到。
例如,若 k = 3 ,则字符串 ((**()*(*))*)(***) 是符合规范的超级括号序列,但字符串 *() 、(*()*) 、((**))*) 、(****(*)) 均不是。特别地,空字符串也不被视
为符合规范的超级括号序列。
现在给出一个长度为 n 的超级括号序列,其中有一些位置的字符已经确定,另外一些位置的字符尚未确定(用 ? 表示)。小 w 希望能计算出:有多少种将所有尚未确定的字符一一确定的方法,使得得到的字符串是一个符合规范的超级括号序列?
可怜的小 c 并不会做这道题,于是只好请求你来帮忙。
【输入格式】
从文件 bracket.in 中读入数据。
第 1 行,2 个正整数 n, k 。
第 2 行,一个长度为 n 且仅由 ( 、) 、*、? 构成的字符串 S 。
【输出格式】 计算机技术代写
输出到文件 bracket.out 中。
输出一个非负整数表示答案对 109 + 7 取模的结果。
【样例 1 输入】
第 6 页 共 13 页2021 CCF 非专业级软件能力认证 CSP-J/S 2021 第二轮认证
括号序列(bracket)
1 7 3
2 (*??*??
【样例 1 输出】
1 5
【样例 1 解释】
如下几种方案是符合规范的:
1 (**)*()
2 (**(*))
3 (*(**))
4 (*)**()
5 (*)(**)
【样例 2 输入】
1 10 2
2 ???(*??(?)
【样例 2 输出】
1 19
【样例 3】
见选手目录下的 bracket/bracket3.in 与 bracket/bracket3.ans。
【样例 4】
见选手目录下的 bracket/bracket4.in 与 bracket/bracket4.ans。
【数据范围】
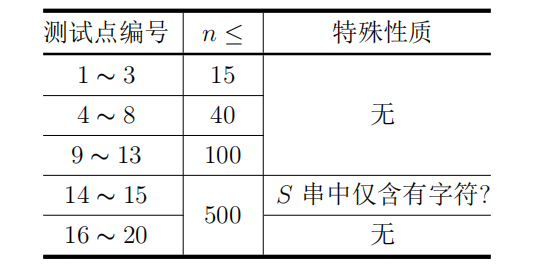
对于 100% 的数据,1 ≤ k ≤ n ≤ 500 。
回文(palin)
【题目描述】
给定正整数 n 和整数序列 a1, a2, . . . , a2n,在这 2n 个数中,1, 2, . . . , n 分别各出现恰好 2 次。现在进行 2n 次操作,目标是创建一个长度同样为 2n 的序列 b1, b2, . . . , b2n,初始时 b 为空序列,每次可以进行以下两种操作之一:
- 将序列 a 的开头元素加到 b 的末尾,并从 a 中移除
- 将序列 a 的末尾元素加到 b 的末尾,并从 a 中移除
我们的目的是让 b 成为一个 .回 .文 .数 .列,即令其满足对所有 1 ≤ i ≤ n,有 bi = b2n+1−i。
请你判断该目的是否能达成,如果可以,请输出字典序最小的操作方案,具体在【输出格式】中说明。
【输入格式】 计算机技术代写
从文件 palin.in 中读入数据。
每个测试点包含多组测试数据。
输入的第一行包含一个整数 T,表示测试数据的组数。
每组测试数据的第一行包含一个正整数 n,第二行包含 2n 个用空格隔开的整数a1, a2, . . . , a2n。
【输出格式】
输出到文件 palin.out 中。
对每个测试数据输出一行答案。
如果无法生成出回文数列,输出一行 ‐1,否则输出一行一个长度为 2n 的、由字符L 或 R 构成的字符串(不含空格),其中 L 表示移除开头元素的操作 1,R 表示操作 2。
你需要输出所有方案对应的字符串中字典序最小的一个。
字典序的比较规则如下:长度均为 2n 的字符串 s1..2n 比 t1..2n 字典序小,当且仅当存在下标 1 ≤ k ≤ 2n 使得 ∀1 ≤ i < k 有 si = ti 且 sk < tk。
【样例 1 输入】
1 2
2 5
3 4 1 2 4 5 3 1 2 3 5
4 3
5 3 2 1 2 1 3
【样例 1 输出】
1 LRRLLRRRRL
2 ‐1
【样例 1 解释】
在第一组数据中,生成的的 b 数列是 4 5 3 1 2 2 1 3 5 4,可以看出这是一个回文数列。
另一种可能的操作方案是 LRRLLRRRRR,但比答案方案的字典序要大。
【样例 2】
见选手目录下的 palin/palin2.in 与 palin/palin2.ans。
【数据范围】 计算机技术代写
令∑n 表示所有 T 组测试数据中n 的和。
对所有测试点保证1≤ T ≤ 100, 1 ≤ n,∑n ≤ 5 × 105。
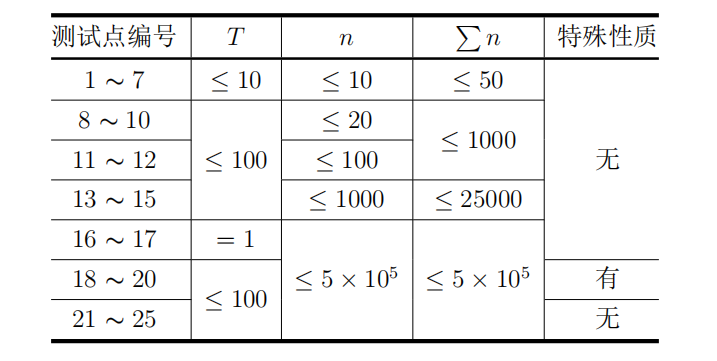
特殊性质:如果我们每次删除 a 中两个相邻且相等的数,存在一种方式将序列删空(例如 a = [1, 2, 2, 1])。
交通规划(traffffic)
【题目描述】
给定一个平面上 n 条水平直线和 m 条垂直直线,它们相交形成 n 行 m 列的网格,从上到下第 r 条水平直线和从左到右第 c 条垂直直线之间的交点称为格点 (r, c)。网格中任意两个水平或垂直相邻的格点之间的线段称为一条边,每条边有一个非负整数边权。
进行 T 次询问,每次询问形式如下:
给出 k(T 次询问的 k 可能不同)个附加点,每个附加点位于一条从网格边缘向外出发的射线上。所有从网格边缘向外出发的射线按左上-右上-右下-左下-左上的顺序依次编号为 1 到 2n + 2m,如下图:
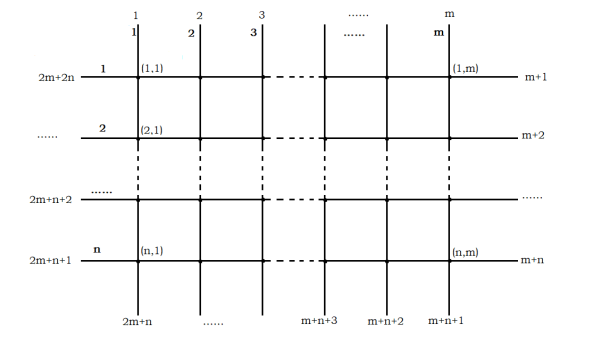
图 2: 射线的编号
对于每次询问,不同附加点所在的射线互不相同。每个附加点和最近的格点之间的线段也称为一条边,也有非负整数边权(注意,在角上的格点有可能和两个附加点同时相连)。
给定每个附加点的颜色(黑色或者白色),请你将网格内每个格点的颜色染成黑白二者之一,并使得所有两端颜色不同的边的边权和最小。请输出这个最小的边权和。
【输入格式】
从文件 traffffic.in 中读入数据。
第一行 3 个正整数 n, m, T 分别表示水平、垂直直线的数量,以及询问次数。
接下来 n − 1 行,每行 m 个非负整数。其中第 i 行的第 j 个非负整数 x1i,j 表示(i, j) 和 (i + 1, j) 间的边权。
接下来 n 行,每行 m − 1 个非负整数。其中第 i 行的第 j 个非负整数 x2i,j 表示(i, j) 和 (i, j + 1) 间的边权。
接下来依次输入 T 组询问。第 i 组询问开头为一行一个正整数 ki 表示这次询问附加点的总数。接下来 ki 行每行三个非负整数。其中第 j 行依次为 x3i,j , pi,j , ti,j 表示第 i 个附加点和相邻格点之间的边权、所在的射线编号以及附加点颜色(0 为白色,1 为黑色)。保证同一组询问内 pi,j 互不相同。
每行的多个整数由空格分隔。
【输出格式】 计算机技术代写
输出到文件 traffffic.out 中。
输出 T 行,第 i 行输出一个非负整数,表示第 i 次询问染色之后两端颜色不同的边权和的最小值。
【样例 1 输入】
1 2 3 1
2 9 4 7
3 3 8
4 10 5
5 2
6 19 3 1
7 17 9 0
【样例 1 输出】
1 12
【样例 1 解释】
最优方案:(1, 3),(1, 2),(2, 3) 为黑色;(1, 1),(2, 1),(2, 2) 为白色。
【样例 2】
见选手目录下的 traffffic/traffffic2.in 与 traffffic/traffffic2.ans。
【样例 3】
见选手目录下的 traffffic/traffffic3.in 与 traffffic/traffffic3.ans。
【样例 4】
见选手目录下的 traffffic/traffffic4.in 与 traffffic/traffffic4.ans。
【样例 5】
见选手目录下的 traffffic/traffffic5.in 与 traffffic/traffffic5.ans。
【数据范围】
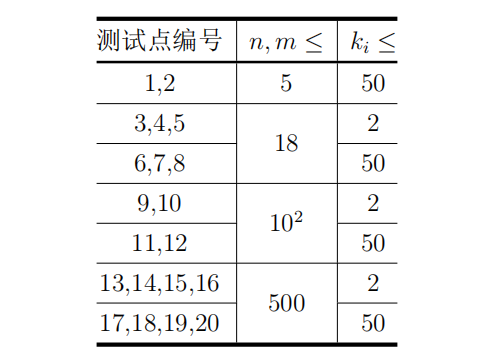
对于所有数据,2 ≤ n, m ≤ 500, 1 ≤ T ≤ 50, 1 ≤ ki ≤ min{2(n + m), 50}, 1 ≤ ∑Ti=1ki ≤ 50, 0 ≤ x ≤ 106, 1≤ p ≤ 2(n + m), t ∈ {0, 1}。
保证对于每个i ∈ [1, T],pi,j 互不相同。




