CS529 – Spring
Lattices in Computer Science
Homework 3
计算机科学作业代写 You must submit your solutions as a single .pdf file (for Problems 1 and 2) and a single .py file (for Problem 3) on Canvas with…
Instructions:
- You must submit your solutions as a single .pdf file (for Problems 1 and 2) and a single .py file (for Problem 3) on Canvas with your name at the top of both. Typesetting your written solutions using LATEX is strongly encouraged but not required.
- You are welcome to discuss the problems in groups, but you must write up and submit your own solutions. You must also write the names of everyone in your group on the top of your submission.
- If you get stuck you may use any resources that you wish. However, please make sure to cite your sources and explain what you used them for.
- There are 3 questions, worth a total of 30 points.
Problems: 计算机科学作业代写
Problem 1. CVPP via Babai with HKZ-reduced bases,1 14 points
A basis B = (b1, . . . , bn) of a lattice L is said to be HKZ-reduced if it satisfies the following two conditions:
i.∥b1∥ = λ1(L),
ii.For i ∈ {1, . . . , n − 1}, (πi(bi+1), . . . , πi(bn)) is an HKZ-reduced basis of the lattice πi(L), where πi denotes projection onto span(b1, . . . , bi−1)⊥ (and π1 is the identity map).
An HKZ-reduced basis is one way of formalizing what it means to be a “shortest possible basis,” and moreover every lattice has an HKZ-reduced basis. (You may use this fact without proof.) In the problem below, we take B = (b1, . . . , bn) to be an HKZ-reduced basis, and use C to denote a positive constant (not necessarily the same constant at each use).

1.3 Use Equation (2) to show that for all j ∈ {2, . . . , n},
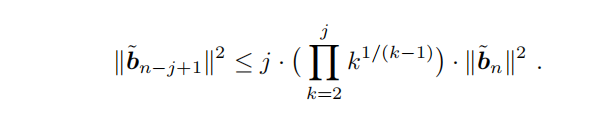
(Hint: Use a proof by induction on j. For the inductive case, apply the induction hypothesis to each term ∥˜bn−k+1∥2in the product in Equation (2), and then rearrange the terms in the resulting double product. This part of theproblem is relatively more challenging, and you may simply assume Equation (3) in the subsequent parts even if you are not able to solve it.)
1.4 Use Equation (3) to conclude that for every j ∈ [n], max1≤j≤n(∥bj∥/∥bn∥)2 ≤ n ln n+C .
(Hint: You may look up bounds on Hn, the sum of the first n terms in the harmonic series.)
1.5 Show that the “prefix basis” (b1, . . . , bi) is also an HKZ-reduced basis for every i ∈ {1, . . . , n}, and
note that this implies max1≤j≤i≤n(∥bj∥/∥bi∥)2 ≤ n ln n+C by Subproblem 1.4. Conclude that there is an(n ln n+C )-approximation algorithm for CVPP.2
(Hint: Recall the approximation factor γ guaranteed by Babai’s algorithm.)
Problem 2. Solving random subset sum with a better approximate CVP oracle, 6 points 计算机科学作业代写
Suppose that there exists a polynomial-time algorithm for solving n 100-approximate CVP. Show that there exists a polynomial-time algorithm for solving random subset sum instances with density O(1/ log n) with high probability over the choice of instance.
(Hint: Adapt the proof of Theorem 2 in the “Solving Random Low-Density Subset Sum Using Babai’s Algorithm”
lecture. What should the new values of γ, β, and N be?)
Problem 3. Using fp(y)lll to break knapsack cryptography, 10 points. 计算机科学作业代写
3.1 Download and install fpylll from https://github.com/fplll/fpylll. (You may also get fpylll from the SageMath package or use fplll instead of fpylll.)
3.2 Look at the tutorial on fpylll at https://github.com/fplll/fpylll/blob/master/docs/tutorial. rst.
(Hint: fpylll uses row bases instead of column bases. That is, the lattice generated by a basis in fpylll is the set of all integer linear combinations of its rows. It is easy to go back and forth between row and column bases by taking the matrix transpose. However, note that the coefficient vector xT of a row basis B multiplies the matrix on the left: in this case, xT B is a lattice vector.)
3.3 Look at the skeleton code in knapsack.py. What you need to fill out is at the bottom of the file.
Construct a basis B and target t from the provided values of a and s using the reduction that we saw in class.3 You may construct these from a and s by hand, or use Python code (including fpylll, NumPy, or any other package that you wish) to do so. The latter is recommended.
3.4 Use the CVP.closest vector function from fpylll to find a closest lattice vector v in L(B) to t.
From v, find the secret binary message vector x. Finally, binary vec to ascii str to convert x into anASCII string, and print this string (this last part is already implemented for you).
(Hint: Although fpylll has an implementation of Babai’s algorithm, it appears to have some issues, so we are using fpylll’s exact CVP solver instead. See https://github.com/fplll/fpylll/blob/master/docs/tutorial. rst#svp-and-cvp-tools for how to use the CVP.closest vector function. Make sure that you pass a row basis to CVP.closest vector.)




