COMP9024 Final Exam (22T0)
计算机Final代考 By starting this exam you acknowledge that you are fit to sit the exam and cannot apply for Special Consideration for issues…
By starting this exam you acknowledge that you are fit to sit the exam and cannot apply for Special Consideration for issues that existed prior to the exam.
If during the exam a circumstance arises that prevents you from completing the exam, please email [email protected] immediately and apply for special consideration shortly after.
Before your final exam, you should read the section “Important Information for Online Assessments” on the Special Consideration webpage. It contains information on what you should do if you experience a technical issue that is beyond your control and impacts your ability to complete an assessment – in particular, how and what to document for a special consideration application.
Admin 计算机Final代考
Marks Contributes 50% towards your final mark
Submit See the submission instructions for each question
Date and time Saturday 05 February 2pm-5pm
Total Marks 50
Structure
This exam consists of two parts:
Part 1: Short Answer questions (25 marks)
Part 2: Programming questions (25 marks)
Notes: 计算机Final代考
Answer all questions. Questions may not be worth equal marks. Questions may be answered in any order.
All answers must be submitted online using the provided instructions in the respective questions.
For programming questions, please note that marks are awarded primarily for your solution algorithm, not just for getting the correct final answer.
Part 1 (of 2): Short Answer Questions (25 marks)
Question 1 (3 marks)
An algorithm solves a problem of size n recursively by breaking it down into two subproblems of size n / 2 with the same structure, until the size of a subproblem is one or zero. It takes O(1) time to convert a problem of size n into two subproblems and it takes O(1) time to combine the results of two subproblems of size n into the result of the problem. What is the time complexity of this algorithm? Justify your answer.
Write your answer in q1.txt (download using “Save As” or similar).
Question 2 (3 marks) 计算机Final代考
An algorithm for solving a problem runs in exponential time O(2n). Suppose that your computer, running an implementation of this algorithm, can process an input of size 10 in one day. What is the maximum input size that can be processed in one day by a computer that is 1000 times faster if it uses the same implementation? Justify your answer.
Write your answer in q2.txt (download using “Save As” or similar).
Question 3 (3 marks)
Consider the the following 2-3-4 tree :
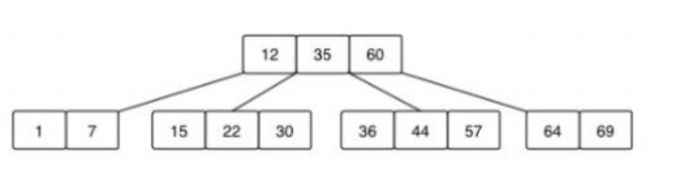
(a) What value(s) would be stored in the root node of the above 2-3-4 tree after the insertion of the value 8? What value(s) would be stored in the node that now contains 8?
Note: if you need to promote a value, you must promote the smaller value from the available alternatives (if any). Justify your answer.
(b) What value(s) would be stored in the root node of the above 2-3-4 tree after the insertion of the value 50? What value(s) would be stored in the node that now contains 50? Note: if you need to promote a value, you must promote the smaller value from the available alternatives (if any). Justify your answer.
Write your answer in q3.txt (download using “Save As” or similar)..
Question 4 (4 marks)
Suppose that you need to implement a Priority Queue ADT that provides the following operations:
- Push: Adds a new key-element pair
- Pop: Remove a key-element pair with highest priority
- PrintInOrder: Prints all the key-element pairs in non-increasing order of priority
Assuming that all three operations will be frequently used, which one of the following data structures is most suitable? Justify your answer. You must use time complexities as a basis for your justification. 计算机Final代考
- Ordered Linked List
- Ordered Array
- AVL Tree
- Hashtable
- Heap
Write your answer in q4.txt (download using “Save As” or similar)..
Question 5 (3 marks)
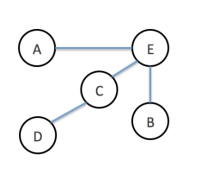
While constructing the above minimum spanning tree, the edges were added in the following sequence:
- A – E
- C – D
- E – B
- E – C
Which one of the following algorithms discussed in the lectures was used to construct the above minimum spanning tree? Justify your answer.
- Depth First Algorithm
- Dijkstra’s Algorithm
- Prim’s Algorithm
- Kruskal’s Algorithm
Write your answer in q5.txt (download using “Save As” or similar)..
Question 6 (3 marks) 计算机Final代考
A binary search tree contains the values 2, 7, 8, 10, 14, 16, 20, 24, 33, and 40. A preorder traversal produces the sequence: 16, 10, 7, 2, 8, 14, 24, 20, 40, 33. Which one of the following sequences will be produced by a valid post-order traversal of the same tree? Briefly explain your answer.
- 2, 7, 8, 14, 10, 20, 33, 40, 24, 16
- 2, 8, 7, 14, 10, 20, 33, 40, 24, 16
- 2, 7, 8, 14, 10, 20, 33, 24, 40, 16
- 2, 7, 8, 10, 14, 20, 24, 33, 40, 16
- None of the other choices are correct.
Write your answer in q6.txt (download using “Save As” or similar)..
Question 7 (3 marks)
Which of following statements about tries is not correct? Briefly explain your answer.
- Searching for a word in a standard trie takes O(m) time, where m is the length of the longest word in the trie.
- In a trie, no word can be a prefix of another word.
- In a standard trie, each leaf node corresponds to a word.
- A compressed trie is used to save memory for storing words.
Write your answer in q7.txt (download using “Save As” or similar)..
Question 8 (3 marks) 计算机Final代考
Which of the following statements about the Knuth-Morris-Pratt (KMP) algorithm is not correct?
- The time complexity of the KMP algorithm is O(m + n), where m and n are the sizes of the pattern and the text, respectively.
- The KMP algorithm is optimal in terms of time complexity.
- When checking if the pattern occurs at a character in a text, the KMP algorithm always compares the first character of the pattern with the corresponding character in the text.
- The failure function can be computed in O(m) time, where m is the size of the pattern.
Write your answer in q8.txt (download using “Save As” or similar)..
Part 2 (of 2): Programming Questions (25 marks)
Notes
- You can implement as many helper functions as you need. 计算机Final代考
- Note: If you get a “permission denied” error when you try to run the autotest script, you must first make the script executable using the command:
chmod +x autotest
- You can use any code provided in lectures, tutorials, and practice question solutions.However, you must acknowledge the source (e.g., indicate the lecture slide, tutorial question, etc.) in a comment.
- You must test your solutions on the CSE system (e.g., via VLAB or SSH) before making your final submission. This avoids issues due to different testing environments. If you do not do this, you are accepting that even if you have passed the autotests on your local machine, your code may contain errors that were not detected on your machine (e.g., due to differing architectures) that may cause it to fail tests during marking.
Part 2: Q1 (12 Marks)
Your task for this question is to implement the following function in the file nodesNotBalanced.c.
int nodesNotBalanced(BSTree t);
The function nodesNotBalanced(BSTree t) takes one argument: a binary search tree t, and returns the number of nodes that are not height balanced.
For this question, as discussed in the lectures (see here), we say the height of a tree is equal to the maximum path length from the root to a leaf node. A node is not height balanced if the absolute difference between the heights of its left subtree and right subtree is greater than one. The height of an empty tree is -1.
Important: 计算机Final代考
- You must not modify the given tree.
- The time complexity of your solution must be O(n), where n represents the number of nodes in the tree. If your solution is slower than O(n), the maximum mark you can attain for this question will be 5 (out of 12).
- You must not use any arrays or call malloc (or any of its variants). If you don’t satisfy this requirement, you will receive zero for this question.
- Note that the provided autotest does not check the time complexity of your solution and does not check whether you are using arrays or malloc. Hence, you must check that you have met these requirements yourself.
- You can only submit one file, nodesNotBalanced.c. So all your code must be in this file.
Download
Click here to download the zip file for this question.
Alternatively, if you are connected to the CSE system (e.g., via VLAB or SSH), you can copy the zip file using the following command:
$ cp /home/cs9024/public_html/22T0/finalexam_98245609835223841/FinalExam22T0/q1-files.zip .
The Files 计算机Final代考
BSTree.c Contains the implementation of basic binary search tree functions.
BSTree.h Contains the definition of the binary search tree data structure and function prototypes.
testNodesNotBalanced.c The test driver program. The program reads tree data from stdin, calls nodesNotBalanced, and outputs the answer to stdout. You must carefully study how your function is tested by testNodesNotBalanced.c. You can find out more about the behaviour of the testNodesNotBalanced program by looking at the files testNodesNotBalanced.c, autotest and the files in the tests directory. The files named X.in contain sample inputs for the test program and the corresponding expected outputs are in files named X.exp.
nodesNotBalanced.c Contains nodesNotBalanced, the function you must implement.This is the only file you should modify.
Makefile A Makefile to compile your code
tests/ A directory containing the inputs and expected outputs for some basic test cases
autotest A script that uses the tests in the tests directory to autotest your solution. You should only run this after you have tested your solution manually.
Examples
The following examples show the expected output for some different trees. The nodes that are not height balanced are shown in bold.



Testing 计算机Final代考
You can compile and test your function using the following commands:
$ make # builds the testNodesNotBalanced program $ ./autotest # applies all the tests in the tests directory to the testNodesNotBalanced program # applies only one given test case from the tests directory to the testNodesNotBalanced program $ ./autotest test-number
You can find out more about the behaviour of the testNodesNotBalanced program by looking at the files testNodesNotBalanced.c, autotest and the files in the tests directory. The files named X.in contain sample inputs for the test program and the corresponding expected outputs are in files named X.exp.
For example, if you want to run test case 2, use the following command:
$ ./autotest 2
If you want to run all the sample test cases provided, use the following command: 计算机Final代考
$ ./autotest
After you run the tests, additional files will appear in the tests directory. X.out contains the output from running test X.
You can add debugging code to nodesNotBalanced.c or testNodesNotBalanced.c if you want, however, make sure that you remove it before testing and submitting, otherwise your output won’t match the expected output and you’ll fail all the tests. You can also add any auxiliary functions to nodesNotBalanced.c that you think are necessary.
Once you are satisfied with your solution, submit it through the give command or via WebCMS (click here).
The give command is:
$ give cs9024 exam_q9 nodesNotBalanced.c
Please note that the submission script does not run any tests on your program. Thus, it is important that you test your program on the CSE system before submitting.
Make sure you thoroughly test your program! We will run further tests on your submission after the exam which may test different cases from the tests provided to you.
Part 2: Q2 (13 Marks) 计算机Final代考
Your task for this question is to implement the following function in the file rankPopularity.c.
void rankPopularity(Graph g, int src, double *mnV);
The function rankPopularity takes three arguments: a directed graph g, a source node src and an array mnV. For each node v that is reachable from src, the function should store its popularity rank in the array mnV at index v. For example, if node 2 is reachable from src, then when the function returns, mnV[2] should contain the popularity rank of vertex 2.
Popularity rank: Calculate a node’s popularity rank using the following equation:
popularityRank(v) = (inDegree(v) / outDegree(v))
If outDegree(v) is zero, replace it with 0.5.
Please read the example below for more clarifications.
Important notes: 计算机Final代考
- If a node is not reachable from src, the function should not calculate and store the popularity rank for that node. In other words, only nodes reachable from src are considered, and your function must not calculate and store popularity rank values for nodes not reachable from src. In the test program testRankPopularity.c, initially all values in mnV are set to -1. If a node is not reachable from src, the function must not change the corresponding value in mnV (i.e., it should remain as -1), otherwise you will fail that test case.
- You can assume that the mnV array is large enough to store all the required popularity ranks. You can also assume that the given graph g will not have self-loops or parallel edges.
- You must properly use either the DFS or BFS graph traversal algorithm in your solution. Otherwise, you will receive zero marks for this question.
- There is no time complexity requirement for this question.
- Note that the provided autotest does not check whether you are properly using DFS or BFS. Therefore, you must check that you have met this requirement yourself.
- You can only submit one file: rankPopularity.c. So all your code must be in this file.
- As discussed in the lectures, nodes are identified by integers between 0 and nV – 1 (inclusive), where nV is the number of nodes in the graph.
Download
Click here to download the zip file for this question. 计算机Final代考
Alternatively, if you are connected to the CSE system (e.g., via VLAB or SSH), you can copy the zip file using the following command:
$ cp /home/cs9024/public_html/22T0/finalexam_98245609835223841/FinalExam22T0/q2-files.zip .
The Files
Graph.c Contains the implementation of basic Graph ADT functions.
Graph.h Contains the definition of the Graph ADT and function prototypes.
testRankPopularity.c The test driver program. The program reads data, creates a Graph and calls the function rankPopularity, and outputs the answer to stdout. You must carefully study how your function is tested by testRankPopularity.c. You can find out more about the behaviour of the testRankPopularity program by looking at the files testRankPopularity.c, autotest and the files in the tests directory. The files named X.in are input files for the test program testRankPopularity and the corresponding expected outputs are in files named X.exp.
rankPopularity.c Contains rankPopularity, the function you must implement. This is the only file you should modify.
Makefile A Makefile to compile your code
tests/ A directory containing the inputs and expected outputs for some basic test cases
autotest A script that uses the tests in the tests directory to autotest your solution.You should only run this after you have tested your solution manually. Note that this script only tests simple cases. You need to extensively test your program for a wide range of test cases.
Examples
For example, consider the following graph:
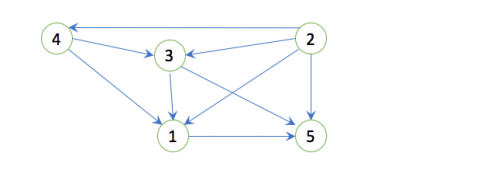
Popularity ranks for nodes reachable from node “4” in the above graph are:
- popularityRank(1) = 3/1 = 3
- popularityRank(3) = 2/2 = 1
- popularityRank(4) = 1/2 = 0.5
- popularityRank(5) = inDegree(5) / outDegree(5). Here, inDegree(5) is 3 and outDegree(5) is 0. So we need to replace outDegree(5) by 0.5 in the above equation, resulting in popularityRank(5) = (3) / (0.5) = 6.
Note that node “2” is not reachable from node “4”, so it must be ignored.
Testing 计算机Final代考
You can compile and test your function using the following commands:
$ make # builds the required testRankPopularity program $ ./autotest # applies all the tests in the tests directory to the testRankPopularity program # applies only one given test case from the tests directory to the testRankPopularity program $ ./autotest test-number
You can find out more about the behaviour of the testRankPopularity program by looking at the files testRankPopularity.c, autotest and the files in the tests directory.
The files named X.in contain sample input for the test program and the corresponding expected outputs are in files named X.exp.
For example, if you want to run test case 2, use the following command:
$ ./autotest 2
If you want to run all the sample test cases provided, use the following command:
$ ./autotest
After you run the tests, additional files will appear in the tests directory. X.out contains the output from running test X.
You can add debugging code to rankPopularity.c or testRankPopularity.c if you want, however, make sure that you remove it before testing and submitting, otherwise your output won’t match the expected output and you’ll fail all the tests. You can also add any auxiliary functions to rankPopularity.c that you think are necessary.
Once you are satisfied with your solution, submit it through the give command or via WebCMS (click here). 计算机Final代考
The give command is:
$ give cs9024 exam_q10 rankPopularity.c
Please note that the submission script does not run any tests on your program. Thus, it is important that you test your program on the CSE system before submitting.
Make sure you thoroughly test your program! We will run further tests on your submission after the exam which may test different cases from the tests provided to you.



