贝尔定理代写 The Baire Category Theorem

Part 1. The Baire Category Theorem.

贝尔定理代写 1.1 Recall the meaning of all the notions used in the statement of Baire Theorem. (Thm I.13.1: Let E be a complete metric space.

1.1 Recall the meaning of all the notions used in the statement of Baire Theorem. (Thm I.13.1: Let E be a complete metric space. If (??)?≥1 is a sequence of dense open sets of E(i.e. ?? = E, ∀? ≥ 1), then ⋂?≥1?? is dense in E)

1.2 Definition: Let (E, d) be a metric space. E is a Baire space if every sequence (Uu)uN of open sets of E such that

Remark: By thm I.13.1, any complete metric space is a Baire Space.

1.4 Let (E, d) be a Baire space and A⊂E.

Definition: 1) A is a residual set if A contains a countable intersection of dense open set in E.

2) A is a meager set (or set of first category) if A is contained in a countable union of closed sets of E with empty intersections.

Show that A is meager set iff Ac is residual.

1.5 a) Show that ℚ forms a meager subset of ℝ.

b) Show using the Baire category theorem, that ℚ? = ℝ\ℚ is not meager. 贝尔定理代写

1.6 (E, d) is a metric space,

Definition: 1) A subset A⊆E is a F -set if A is a countable union of closed sets.

2) A subset A⊆E is a G -set if A is a countable intersection of open sets.

Then, a) show that every closed set of (E, d) is a G -set and every open set of (E, d) is a F -set.

b) let (ℝ, d = ||). That ℚ ⊂ ℝ is a F -set and therefore ℚ? is a G -set. c) using the Baire category theorem, show that ℚ? is not a F -set.

Part 2. Application of Baire Category theorem. 贝尔定理代写

2.2 (Application of 2.1)

Let f : ℝ  ℝ be a differentiable function and let f’ be derivative. Show that the subset of points x  ℝ such that f’ is continuous at x is dense in ℝ.

(Hint: for all u ≥ 0, let ??: ℝ → ℝ

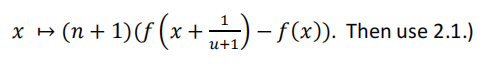
2.3 Use Baire category theorem to show that { f C([0, 1]); f nowhere differentiable in [0, 1]} is dense in C([0, 1]), with respect to the sup norm.

Recall: see for example thm 4.4 of the annexed paper. You can use this proof or any other one, as long as you indicate your reference, but you have to complete the detail, and to write them down in your assignment.

General comment: 贝尔定理代写

Everything you write should be justified. You have to show me that you have understood all the argument you use.