近似向量代写 函数代写 数学代写

Problem 1

近似向量代写 We have established this semester that you may represent a given function via an approximation. You will learn more…

We have established this semester that you may represent a given function via an approximation. You will learn more about this (and the accompanying quantification of the error) in your numerical methods course. For now, we shall look at a given function and its approximation, performing a thorough analysis of the error with the approximation as a function of the ”step”.

This assignment is not mandatory. It exists to give some extra points back to those who feel their current performance in the course is not as they hoped. All work submitted  must  be  your  own  work,  copying in any form will not be tolerated. Satisfactory completion of this assignment will lead to up to 15 bonus points to make up for lost points on old homework assignments. 近似向量代写

You may represent the following equation,

y = 1 − x²

using the following approximation in a MATLAB for-loop 近似向量代写

y_approx(i) = y(i − 1) − 2 · x(i) · ∆x

In a short MATLAB script, complete the following.

(a) Createa vector with 10000 terms in the range [0,1] to represent the ”true”  Call this vector y.

(b) Create approximate vectors in the range [0,1] (Hint: Use the 0:dx:1 syntax, where dx represents ∆x)for the following values of ∆x:

(i) ∆x = 0.001

(ii) ∆x = 0.01

(iii) ∆x = 0.1

(iv) ∆x = 0.25

(c) For each of these approximations, compute the absolute error at x = 1 using the following equation:

Error = |y_true − y_approx|

Using fprintf, create a table which displays: 近似向量代写

(i) Thevalue of ∆x

(ii) Thetrue value of y at x = 1

(iii) Theapproximated value of y at x = 1

(iv) Thevalue of the absolute error at x = 1

This will yield four separate approximation vectors. 近似向量代写

(d) Plotthe true solution using a solid black  Plot the approximations on the same graph along with it. Make sure to include a title, axis labels, and a legend to indicate which line represents each approximation. Change the font name to ”Times” and change lines from 10-15.

(e) In a short (100 word) comment, compare the different approximations. Are they all good? Are some incredibly poor?   Are some imperfect, but good enough for the time savings?   Think about this from a practical, real-world application. Sometimes computational time may be very expensive, and thus it may be advantageous to go with a calculation which is ”good enough”, but significantly computationally  近似向量代写

For your reference, here is an example of the general trends of how the plot should look. The lines from your plots should look similar to this. The formatting of your plot will look different, as this example is purely for the line behavior.

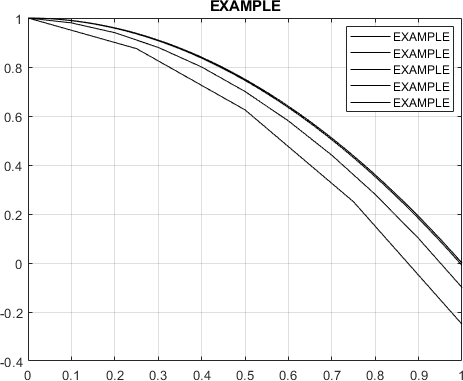
Figure 1: Example of How Lines Should Look