2.2.3造型语意量化模型构建
量化模型代写 基于数量化I型理论的造型语意量化模型构建 数量化理论方法是多元统计分析的一个分支，其中，数量化Ｉ型理论适用于解决自变量类型均是定类变量，基准变量或因变量是定量变量类型的因素分析以及结果预测问题，通过采用说明性、描述性多变量的方法。。。
（1）基于数量化I型理论的造型语意量化模型构建 数量化理论方法是多元统计分析的一个分支，其中，数量化Ｉ型理论适用于解决自变量类型均是定类变量，基准变量或因变量是定量变量类型的因素分析以及结果预测问题，通过采用说明性、描述性多变量的方法来仿效线性表示式中的因变量变化[40]。
在数量化理论中，通常把定类变量称为项目，把定类变量的各种取“值”称作类目，则在本次研究中，数控机床造型要素即为项目，各要素的典型分类则为类目。设n个样品中，第1个项目x1有r1个类目c11，c12，…，c1r1，第2个项目x2有r2个类目c21，c22，…，c2r2，第m个项目xm有rm个类目cm1，cm2，…，cmrm，则共有
个类目，称
为第 j 项目的第 k 个类目在第 i 个样品中的表现，具体取值见式（3-6）。
（3,6）
式中，当第i个样品中j项目的定性数据为k时取1。将所有构成n×p的阶矩阵记为X，X即为反应矩阵。则用户对感性意象词汇的量化评分值与产品的各个造型要素之间可建立如式（3-7）所示的量化关系：
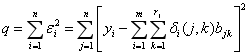
（3,7）
式中 ——仅依赖于j项目之k类目的待定系数；
——第i次抽样的随机误差
基于本次研究课题，构建数量化I型理论的数据矩阵，各参数变量定义见表2-15，数量化I型理论的数据矩阵见表2-16。
式（3-7）中系数的最小二乘估计可基于最小二乘原理求得，即寻求使 量化模型代写
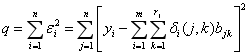
（3-8）
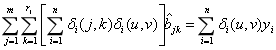
达到最小值。则求q关于buv的偏导数并令其等于0，得到使q达到最小值的bjk，记为b^jk，则b^jk应满足式（3-9）。
（3-9）
将式（3-9）用矩阵形式表示，可写成
（3-10）
式中，
，
。称方程组（3-9）或（3-10）为正规方程（组），求解正规方程（组）各未知数得到的解即为最终构建的模型回归系数。
表2-15 各参数变量 量化模型代写
| 要素项目 | 类目 | 要素项目 | 类目 |
| 防护罩a1 | c11直面 | 观察窗a4 | c41不规则形 |
| c12直面+斜面 | c42圆角矩形 | ||
| c13直面+圆角过渡 | c43直角+圆角 | ||
| c14斜面 | c44直角矩形 | ||
| c15斜面+曲面 | 门a5 | c51同面型 | |
| c16斜面+圆角过渡 | c52凹形 | ||
| c17曲面 | c53凸形 | ||
| c18多形态 | 把手a6 | c61直把手+分体+圆面/椭圆面 | |
| 数控面板a2 | c21镶嵌式 | c62直把手+整体+圆面/椭圆面 | |
| c22立柱式 | c63曲把手+分体+圆面 | ||
| 底座a3 | c31直方块 | c64异形 | |
| c32楔形块体 | |||
| c33凹形 |
表2-16 数量化I型理论数据矩阵
| ID | 统一的 | 现代的 | 简约的 | 粗犷的 | 严谨的 | 安全的 | c11 | c12 | c13 | c14 | c15 | … | c63 | c64 |
| 1 | 1.19 | 0.95 | 0.90 | -0.13 | 1.31 | 1.61 | 0 | 0 | 0 | 0 | 0 | … | 1 | 0 |
| 2 | 1.65 | 1.29 | 1.24 | -0.80 | 1.43 | 1.64 | 1 | 0 | 0 | 0 | 0 | … | 0 | 0 |
| 3 | 1.63 | 1.64 | 1.35 | -0.38 | 1.24 | 1.93 | 0 | 0 | 0 | 0 | 1 | … | 1 | 0 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 17 | 1.60 | 0.70 | 1.11 | 0.13 | 1.41 | 1.86 | 0 | 1 | 0 | 0 | 0 | … | 0 | 0 |
| 18 | 1.40 | 1.68 | 0.95 | -0.58 | 1.34 | 1.73 | 0 | 0 | 1 | 0 | 0 | … | 0 | 0 |
| 19 | 1.67 | 2.44 | 1.33 | -0.78 | 1.67 | 2.00 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 |
| 20 | 2.67 | 2.67 | 2.11 | -0.44 | 2.22 | 2.22 | 0 | 0 | 0 | 0 | 0 | … | 0 | 0 |
同多元线性回归情形一致，数量化I型理论通过计算样本间的复相关系数r来衡量模型进行预测时的精度，见式（2-11）。
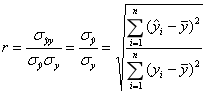
（2-11）
运用Matlab编程实现上述计算，对回归模型系数以及复相关系数进行求解，模型因变量为6个代表性感性意象词汇评分值，自变量为24个造型要素分类。以“统一的”为例，各模型回归系数b、复相关系数r见表2-17所示。 量化模型代写
表2-17 “统一的”模型回归系数及复相关系数
| 回归系数 | 回归系数估计值 | 回归系数 | 回归系数估计值 | 复相关系数r |
| b1 | 3.163 | b13 | 0.713 | 0.9932 |
| b2 | 2.550 | b14 | 已排除 | |
| b3 | 5.578 | b15 | -1.245 | |
| b4 | 5.128 | b16 | -1.600 | |
| b5 | 7.075 | b17 | -1.673 | |
| b6 | 5.315 | b18 | 已排除 | |
| b7 | 5.833 | b19 | 0.113 | |
| b8 | 5.090 | b20 | 1.668 | |
| b9 | 已排除 | b21 | 已排除 | |
| b10 | 0.235 | b22 | -2.638 | |
| b11 | 已排除 | b23 | 5.793 | |
| b12 | 已排除 | b24 | -2.335 |
由表2-17可得“统一的”回归模型为：
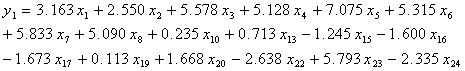
（2-11）
同理可得到其他感性意象词汇的回归方程系数，详见附录6，回归模型为：
“现代的”回归模型：
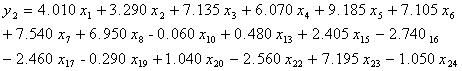（2-12）
“简约的”回归模型：
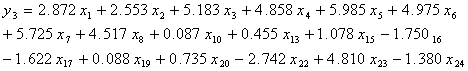
（2-13）
“粗犷的”回归模型：
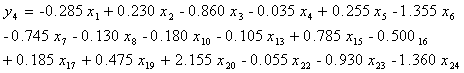（2-14）
“严谨的”回归模型：
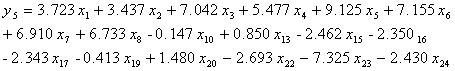
（2-15）
“安全的”回归模型：
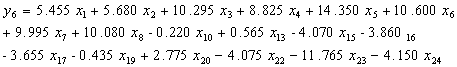（2-16）
式（2-11）至式（2-16）各变量释义见表2-18。
表2-18 回归模型变量释义表 量化模型代写
| 变量 | 释义 | 变量 | 释义 | 变量 | 释义 |
| “统一的”评分 | 斜面+曲面 | 直角+圆角 | |||
| “现代的”评分 | 斜面+圆角过渡 | 直角矩形 | |||
| “简约的”评分 | 曲面 | 不规则形 | |||
| “粗犷的”评分 | 多形态 | 同面型 | |||
| “严谨的”评分 | 镶嵌式 | 凹型 | |||
| “安全的”评分 | 立柱式 | 凸型 | |||
| 直面 | 直方块 | 直把手+分体+圆面 | |||
| 直面+斜面 | 楔形块体 | 直把手+整体+圆面 | |||
| 直面+圆角过渡 | 凹形 | 曲把手+分体+圆面 | |||
| 斜面 | 圆角矩形 | 异形 |
根据数量化I型理论，考虑每一个数控机床项目对因变量的贡献度，可通过指标“偏相关系数”求得，计算方法见式（2-17）至式（2-23）。
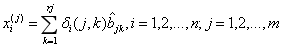
（2-17）
（2-18）
（2-19）
（2-20）
则得到个变量（包括基准变量）之间的样本相关矩阵，见式（2-21）。
（2-21）
（2-22）
以表示的逆矩阵中的元素，见式（2-22），则偏相关系数计算公式见式（2-23）。
（2-23）
通过matlab编程实现上述偏相关系数的计算过程，计算结果见表2-19。
表2-19设计要素项目与感性意象词汇之间的偏相关系数 量化模型代写
| 感性词汇 | 防护罩 | 数控面板 | 底座 | 观察窗 | 门 | 把手 |
| 统一的 | 0.9915 | 0.9885 | 0.7377 | 0.9807 | 0.974 | 0.9904 |
| 现代的 | 0.9992 | 0.9991 | 0.6152 | 0.9985 | 0.9952 | 0.9990 |
| 简约的 | 0.9903 | 0.9856 | 0.3754 | 0.9800 | 0.9142 | 0.9900 |
| 粗犷的 | 0.9890 | 0.5676 | 0.8531 | 0.9764 | 0.9863 | 0.9670 |
| 严谨的 | 0.9966 | 0.9963 | 0.7436 | 0.9948 | 0.9910 | 0.9963 |
| 安全的 | 0.9968 | 0.9967 | 0.8185 | 0.9955 | 0.9931 | 0.9963 |
（2）模型验证 计算相对误差是常用的模型可靠性验证方式，研究将采用此方法完成模型的验证工作。根据已得到的多元回归模型，选取10个样本重新代入模型中获得用户感性意象词汇评分值，作为模型的预测输出，计算预测值与实际期望值的相对误差，见图2-9、图2-10。
由图2-9、图2-10可知，模型相对误差最高为20%，最低小1%，平均相对误差小于13%，以上相对误差值大小均不大于20%，在可接受的误差范围内，则说明模型的可靠性较好。
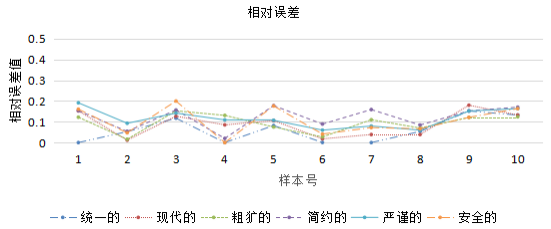
图2-9 相对误差值
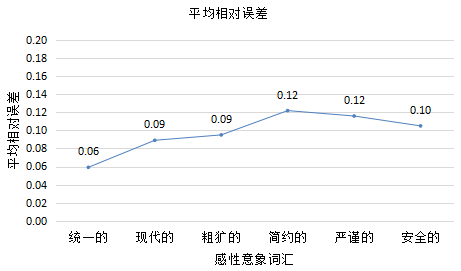
图2-10 平均相对误差值
本章主要完成了代表性感性意象词汇获取与造型语意量化模型构建工作。研究在收集的 140 个感性意象词汇的基础上，通过语意分群实验、多维展开分析、聚类分析获得了代表性感性意象词汇 6 个，分别为统一的、现代的、粗犷的、简约的、严谨的、安全的，作为后续视觉语意量化模型构建的词汇基础。
通过分析国内外数控机床代表品牌，获取了249个产品初始样本；运用形态分析法和层次分析法得到了以防护罩、数控面板、底座、观察窗、门、把手、标识为主的关键造型元素；基于数量化I型理论，对感性意象词汇评分与造型要素之间进行了多元回归分析，得到了两者之间的量化关系，并计算偏相关系数得到了各造型要素对各感性意象词汇评分的贡献度，以及计算复相关系数和相对误差验证了模型的预测精度，得到模型具有较高的可靠性。
更多代写：计算机代写 GMAT代考 经济学代考 教育论文代写 商科代写 英国留学费用
