金融计算代写 MA417代写

MA417 Computational Methods in Finance

Assessed Coursework

金融计算代写 Your coursework must be submitted by Monday 11th May 2020, 4pm (UK time).All consequences regarding late submission…

1 Guidelines 金融计算代写

1.1 Submission

• Your coursework must be submitted by Monday 11th May 2020, 4pm (UK time).
  All consequences regarding late submission can be found on the School’s website

https://info.lse.ac.uk/Staff/Divisions/Academic-Registrars-Division/Teaching-Quality-Assurance-and-Review-Office/Assets/Documents/Calendar/
GeneralAcademicRegulations.pdf

Note in particular: Five marks (out of 100) will be deducted for coursework submitted within 24 hours of the deadline and a further five marks will be deducted for each subsequent 24-hour period (working days only) until the coursework is submitted.
After five working days, coursework will only be accepted with the permission of the Chair of the Sub-Board of Examiners.

• Please submit your report as a PDF-file together with all files containing your C++ code (MA417) or other code (ST433) by email to msc-coursework@maths.lse.ac.uk. Include either “MA417 submission” or “ST433 submission” in the subject line.
• For the electronic submission please only submit one zip-file that contains all your files. Your zip-file should have the following name: If your candidate number is 123456, then name your zip-file MA417 CN123456.zip or ST433 CN123456.zip (depending on whether you are
  registered under MA417 or ST433).

– The project consists of Part A and Part B. Your zip-file must contain your two project reports (as two separate pdf-files) which you should name according to your course code, candidate number and name of the part of the project, e.g.,

MA417 CN123456report PartA.pdf and MA417 CN123456report PartB.pdf or ST433 CN123456report PartA.pdf and ST433 CN123456report PartB.pdf.
– Your zip file must also contain all your C++ code including makefiles and .cbp-files (where necessary) for MA417 and all your code for ST433.

• The content of your work must remain anonymous, so do not write your name on anything except the Plagiarism Statement. Instead, you must identify your work with your Examination Candidate Number. You can check your candidate number on ’LSE for You’.

1.2 Academic integrity 金融计算代写

• When you submit the coursework you must submit a completed and signed copy of the Plagiarism Statement (available on Moodle).
  You are required to read the information on plagiarism on the following website:

https://info.lse.ac.uk/Staff/Divisions/Academic-Registrars-Division/Teaching-Quality-Assurance-and-Review-Office/Assets/Documents/Calendar/
RegulationsAssessmentOffences-Plagiarism.pdf

Note in particular the first paragraph on this website:
“All work for classes and seminars (which could include, for example, written assignments, group work, presentations, and any other work, including computer programs) must be the student’s own work. Direct quotations from other work must be placed properly within quotation marks or indented and must be cited fully. All paraphrased material must be clearly acknowledged. Infringing this requirement, whether deliberately or not, or passing o↵
the work of others as the students own work, whether deliberately or not, is plagiarism.”

• Note that all reports and codes will be submitted to Turnitin for textual similarity review and the detection of plagiarism.
• You must take this assessment completely alone and not show or discuss it with anyone else.
• This is an open book assessment and you are allowed to use any material made available on Moodle for MA417, ST433, MA432, and any academic literature as long as you cite the material that you use fully. 金融计算代写
  For MA417, there are restrictions on the use of libraries for the C++ code, please see below.
• You are not permitted to: consult any other person about the content of the assessment; allow any other person to edit or proof read your work; submit any ideas or phrasing that are not your own (without appropriate citation).
• You should not include any writing of your own that has been submitted for a di↵erent summative assessment.
• The examiners may conduct vivas to check that you were the author of your submitted assessment.

1.3 Structure of the coursework

• This coursework consists of two parts: Part A and Part B.
  Part A and Part B will each count 50% of the final mark for MA417/ST433.
• Part A: Replaces the traditional exam component of the course. Part A is identical for both course codes (MA417 and ST433).
• Part B: Represents the project part of the courses MA417 and ST433. Part B for MA417 is di↵erent from Part B for ST433. All MA417 students have to do Part B for MA417 and all ST433 students have to do Part B for ST433.

1.3.1 Note for resit/deferred candidates 金融计算代写

• All resit/deferred candidates who are due to only sit the exam component of MA417/ST433 this summer, will only do Part A of the coursework.
• All resit/deferred candidates who are due to only do the project component of MA417/ST433 this summer, will only do Part B of the coursework. Note that this will now depend on your course code. If you are a ST433 student, you do Part B for ST433 and if you are an MA417 student, you do Part B for MA417.
• All resit/deferred candidates who are due to sit the exam and do the project, will have to do both parts (Part A and Part B) of this coursework where Part B again depends on the course code.

1.4 Specific guidelines for Part A 金融计算代写

• Part A consists of four problems. Your answers to all four problems will count towards the final mark.
• Part A examines the mathematical part of the course. You are required to use theoretical arguments to answer the questions. You should not use any evidence that you can obtain from implementing the simulation methods as justification for your answers. You are, however, allowed to use calculators/computer code to evaluate an analytical formula for specific model parameters.
• Write a report and not just a question-answer style exercise set solution to answer the questions. Your report should contain all results and their derivation, interpretation and discussion. Use complete sentences throughout. Give detailed arguments to explain your ideas and carefully justify your answers.
• Your answers to Part A must not exceed 20 A4 pages. If you typeset your answers then use a text font of 12 point size and single spacing.

1.5 Specific guidelines for Part B for MA417

• Part B consists of three problems. Your answers to all three problems will count towards the final mark.
• Both your written report and your C++ code will contribute to the final mark.
• Write a report and not just a question-answer style exercise set solution to answer the questions. Your report should contain all results and their derivation, interpretation and discussion. Use complete sentences throughout. Give detailed arguments to explain your ideas and carefully justify your answers. 金融计算代写
• You are required to typeset your answers to Part B. You can use any typesetting programme/software of your choice (LaTeX, MS Word, etc.). Your answers to Part B must not exceed 15 A4 pages (text font of 12 point size and single spacing). Pages will be counted from the first page containing text until the beginning of the appendix. Hence material in the appendix (such as the C++ code), bibliography, title pages, etc. do not count towards the page count

• The only acceptable programming language for Part B for MA417 is C++.You are, however, allowed to use any software of your choice for graphical illustration of the output of your C++ program(s) if you choose to do so.

  You should implement all routines from scratch (using libraries such as iostream, stdlib, cmath) and hence you must not use special scientific/numerical C++ libraries. There is one exception to this rule:
  – You may use C++ code from the MA432 (Programming in C++) and MA417 Programming Sessions provided on the MA432 and MA417 Moodle pages. If you decide to do so just write a comment in your C++ file saying, e.g., the function X or the class Y was taken from the solutions to MA432/MA417 Worksheet Z. 金融计算代写

• In the appendix please provide codes for all your C++ programs with all relevant documentation and instructions to the examiners (such as how to run your programs, usage of parameters, etc.).
• Please note that your C++ program(s) should NOT ask the user to enter variables needed for the computation via the standard input stream. Choose reasonable default parameters yourself (e.g., as global variables) and make clear in your instructions what the meaning and the names of the variables are such that the examiners can test several examples.
• Note that your code will be compiled and tested using Code::Blocks (version 17.02). You are strongly advised to use this programming environment to produce and test your code.
• If you decide to split up your code into several files you are required to submit the corresponding project file (the .cbp file) to enable direct compilation within Code::Blocks.

1.6 Assessment 金融计算代写

Part A and Part B will each count 50% of the final mark for MA417/ST433.
The coursework will be marked in line with the departmental assessment criteria which are available on:

http://www.lse.ac.uk/Mathematics/assets/documents/Assessment-criteria.pdf

2 Coursework Description Part A: MA417 and ST433 金融计算代写

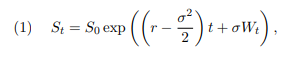
Problem 1. Describe briefly three di↵erent methods for generating a sample from the standard normal distribution. Which one of the three methods would you use and why?
For the remaining part of the coursework we consider the standard Black-Scholes financial market.
Definition 1. We consider a financial market consisting of two assets: The riskless asset has time-t price , where is the constant interest rate, and the risky asset (stock) has time-t price

where S0 > 0 is the initial stock price, is the volatility, is a standard one-dimensional Brownian motion under the risk-neutral measure. We refer to this market as the standard BlackScholes financial market.

Problem 2. Throughout this question we consider the standard Black-Scholes financial market with the following model parameters: S0 = 1, r = 0,

Consider the option whose payo↵ P at the maturity date T = 1 is given by 金融计算代写

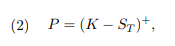
where K = 1/1000. Let X1,…,Xn be i.i.d. random variables with a standard normal distribution. Use the given model parameters for the financial market and the payo↵ of the option to answer all parts of Problem 2.
1. Write down a Monte Carlo estimator for the approximation of the time-0 price of the option with payo↵ P that uses X1,…,Xn. Justify your answer.
2. Write down an antithetic variates estimator for the approximation of the time-0 price of the option with payo↵ P that uses X1,…,Xn. Justify your answer.

3. Does your antithetic variate estimator in part 2 have a strictly smaller variance than your Monte Carlo estimator in part 1? Provide a proof for your answer.

4. Specify a suitable importance sampling estimator for estimating the time-0 price of the option with payo↵ P that performs better (according to a criterion that you should define) than the Monte Carlo estimator from part 1. Argue why the importance sampling estimator is better than the Monte Carlo estimator. 金融计算代写
5. Estimate the time-0 price of the option with payo↵ P by combining the ideas of importance sampling and control variate estimation. To do this, specify a control variable that can be used for reducing the variance of the importance sampling estimator. Write down a formula for this estimator and explain how you can generate the random variables used by this estimator. Discuss properties of this estimator.
6. Which method would you use to estimate the time-0 price of the option with payo↵ P (assuming that you cannot use the analytical formula)? Justify your answer.

Problem 3. We consider an option whose payoff at the maturity date T > 0 is given by

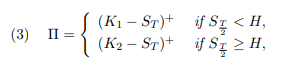
where We want to determine its time-0 price in the standard Black-Scholes financial market.

1. Explain how you can approximate the time-0 price of this option using a Monte Carlo estimator that uses exactly two independent standard normally distributed random variables per sample path. Justify your answer. 金融计算代写
2. Explain how you can approximate the time-0 price of this option using a Monte Carlo estimator that uses exactly one standard normally distributed random variables per sample path. Justify your answer.
3. Which of the two estimators (from parts 1 and 2) has the smaller variance? Justify your answer.

Problem 4. Give an example of a barrier option and describe in detail how you would estimate the time-0 price of the barrier option in the standard Black-Scholes financial market using simulation. Discuss which criterion or criteria you would use to assess how well your method works. Argue
why your proposed method is a suitable choice for the given problem.

3 Coursework Description Part B: MA417 only 金融计算代写

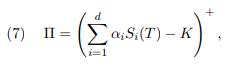
Throughout this project we consider a multivariate Black-Scholes financial market consisting of one riskless asset and risky assets (stocks). All prices are already specified with respect to the risk-neutral measure. The riskless asset has time-t price , where  is the constant
interest rate and the price of stock i (per share) for  at time t is given by

where Si(0) > 0 is the initial stock price and are independent standard one-dimensional Brownian motions under the risk-neutral measure. Furthermore is the Cholesky factor of the positive definite matrix  given by

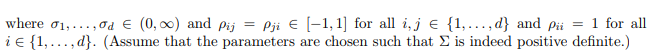
Problem 5. 金融计算代写

1. Write C++ code that computes the Cholesky factorisation for a positive definite
2. Consider d = 3 and defined in (5), where p12 = 0.2, p13= 0.8, p23 = 0.5, Compute the Cholesky factorisation of ⌃ using your C++ code.

Problem 6.

1. Use Ito’s formula to prove that for the stochastic di↵erential equation
dSi(t) = Si(t)

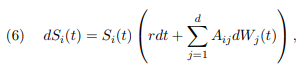
has the solution given in (4).
2. Write down two di↵erent methods for generating sample paths of the stochastic processes Explain which of the two methods you have proposed is more suitable for generating these sample paths and give reasons for your choice.
3. Write a C++ programme that generates sample paths of the stochastic processes on a discrete time grid using one of the two methods considered in part 2. 金融计算代写

Problem 7. Consider the problem of pricing an option which has the payo↵ ⇧ at the maturity date T > 0, where

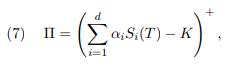
for some constants
1. Explain the relationship between the payoff  and the payo↵ of a standard European call option.

2. Explain how you can approximate the time-0 price of the option with payoff given in (7) using a Monte Carlo estimator and specify an asymptotic confidence interval for the time-0 price of this option based on the Monte Carlo estimator.

3. Write a C++ programme that computes an approximation of the time-0 price of the option with payo↵ ⇧ given in (7) using a Monte Carlo estimator and also gives an asymptotic 95% confidence interval for this time-0 option price.
Give the output of your C++ programme for the following model parameters: d = 3, S1(0) =100, S2(0) = 110, S3(0) = 120, p12 = 0.2, p13 = 0.8, p23 = 0.5,T = 1, K = 100 r = 0.01,

4. Specify one control variate estimator for approximating the time-0 price of the option with payoff  given in (7) and argue why you think this is a suitable choices for the given problem. Write C++ code that implements this control variate estimators. Compare the performance of the control variate estimator to the performance of the standard Monte Carlo estimator. Discuss your findings.