AMATH 250 Online Assignment 2
AMATH代写 Late penalty is 1% per hour. It is your responsibility to make sure you have time to upload your assignment by the deadline.You…
Late penalty is 1% per hour. It is your responsibility to make sure you have time to upload your assignment by the deadline.You may use the course materials posted on the course website and the optional text as references. You are also allowed to discuss ideas with your classmates, the course instructor and TAs. Please do not post fifinal answers or give away too much on Piazza; it will be monitored closely. Your submitted work must be written upon your own and should indicate your knowledge of the material.
Academic Integrity Declaration (AID): Fill out the Academic Integrity Declaration form and upload as a page 1 to Crowdmark. AMATH代写
I declare the following statements to be true:
- The work I submit here is entirely my own
- I have not used any unauthorized aids
- I am aware that misconduct related to examinations can result in signifificant penalties including failing the course and suspension, as outlined in Policy 71
- I have discussed the assignment with the following people (if any):
- Write your name and the date in the box below, then upload this page to Crowdmark.
Each question should be uploaded separately to Crowdmark. AMATH代写
- Use the method of undetermined coeffiffifficients to fifind the solution for each IVP/DE.
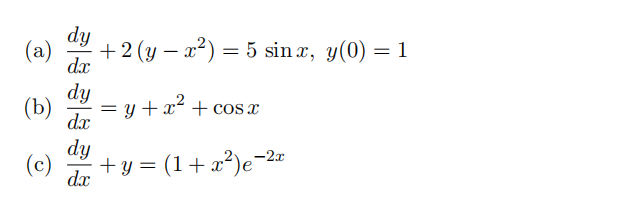
- Even if we are unable to perform the necessary integration, we may be able to express the solutions to di↵erential equations as integrals. The idea is to take advantage of the Fundamental Theorem of Calculus; if we need an anti-derivative of a function f(x), we may always use the expression f(t) dt (and we’re free to choose the value of a arbitrarily).

Using directional fifield analysis on the DE, plot the qualitative behaviour of the solutions. Your plot should demonstrate the qualitative behaviour of all solutions of the DE given y(0) = y0≠ 0.
Hint: First determine the intervals of increase/decrease and intervals of concavity. Then sketch the qualitative shape of the solution for y0≠ 0 in each of those intervals.




