Cryptography & Cryptanalysis
Cryptography代写 Choose two large prime numbers p, q each about 10 bits long, i.e. p, q < 1024 (Use OpenSSL tool obtain these numbers, or search on the Internet)
Asymmetric Key Cryptography
Linux tools to use: OpenSSL, genius
Question 1. Cryptography代写
Choose two large prime numbers p, q each about 10 bits long, i.e. p, q < 1024 (Use OpenSSL tool obtain these numbers, or search on the Internet)
Compute n = pq (2 marks)
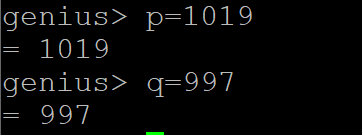
Compute Φ(n) = (p-1)(q-1); discard p, q (2 marks)
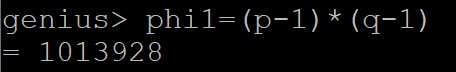
By trial and error choose e such that gcd(e,Φ(n) ) = 1. Then calculate d = e-1 mod kΦ(n)
(2 marks)
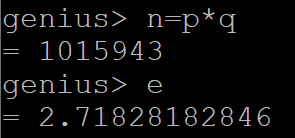
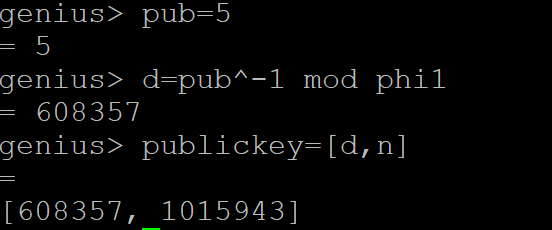
Write down your public key <e,n> and private key is <d,n> (2 marks)
Show your work and results using screen shots. (3 marks)
Assume that you gave Alice your public key to encrypt a message M for you. Choose any message, a number < n and shhow how Alice would encrypt the message M, i.e. (4 marks)
C = Md mod n
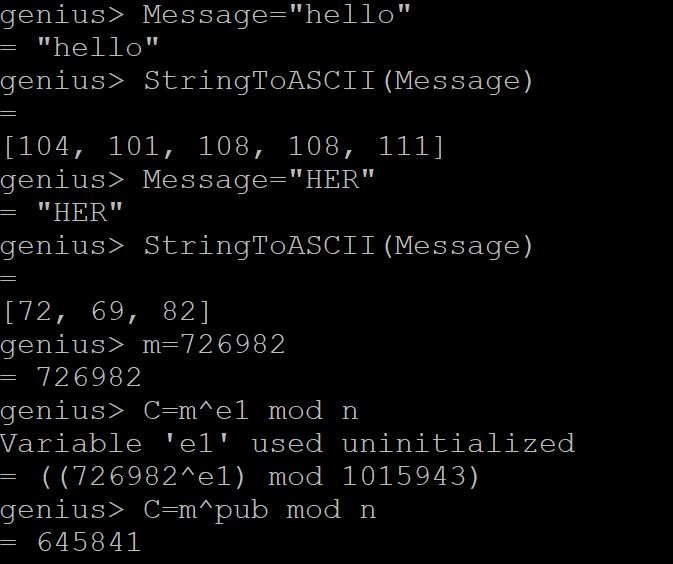
Show how you would decrypt the ciphertext to obtain the plaintext message. (4 marks)
 [ 15 marks]
[ 15 marks]
Question 2. Cryptography代写
One of the most useful applications of public-key cryptography is for the exchange of a session key over an insecure channel which then can be used in a symmetric key algorithm such as AES. Assume that Bob has a pair of public/private keys using the RSA cryptosystem. Develop a simple protocol using RSA which allows the two parties Alice and Bob to obtain a shared secret key. Demonstrate how Alice used the RSA protocol to transport the secret keyword “MostS3cretPa55w@rd” to Bob. Use at least 1024 bits keys.
Who determines the session key in this protocol, Alice, Bob, or both? [10 marks]
Question 3.
RSA encryption and decryption using large numbers. Use the Linux genius math tool. In Linux $ prompt, type $ genius
Note: In genius, hexadecimal values are preceeded with 0x
Given: Alice’s RSA KEY (in hex, 1024 bits)
public exponent e = 7
private exponent, d = 1d1834b810fa0058f403c15515f39baf2a9dcad5c42f32592574650d5369bfec4000dd6f55aa5013e3ab7e347e1d2a4c70f97edf0f9d38043b22069e56bbaa00dd0c6a253b0e4cbc889c56a47d13c934224d4bc6d07d7569d0cd3529ff4c6e3350e05f2ed9885c997cb7337f41ca9a1a8b9815c12e84ce488ae555fb8f4972b7
modulus n = cba9710876d6026eac1a495399a941ca2a508bd85d4a6070062ec35d47e43f75c0060e0b57a8308b39b0736f72cc281716d278196d4c881d9dee2e545f21a607d406a1d2f182a7f39d7878a556c0146db12e2219feef9b0ddfce9d90bc87a5eb3be00dcd68b520d601c52cb545866d4d2edbfb3d26a8d2713dba41324704e0d9
Alice sent her public key <e, n> to Bob. Bob uses it to encrypt a message and send the following ciphertext and sends it to Alice.
Ciphertext, C =
7869635659f29ce2bc427f15e41f5949d8192fed8d8e703ad128f5a9e07a64aa62f92d3d409682e53399379b0bbee73eb3862e8db0f2cc15790274487f25bff88a82f6cdea3483888d4503e4ad4fadaec3e1af7522e0310716442882d0bf03f4256b0c5b744c94f82396a955a779da90f006f36238feda57a03a6291ecdd1285
Show how Alice decrypts and obtains the plaintext. What is the plaintext? [13 marks]
Question 4 Cryptography代写
Breaking RSA with common primes.
Eve is able to monitor all the exchange between Alice and Bob.
If Eve’s public key <eE,nE> and Bob’s public key <eB,nB> share a common factor, they can compute each other’s private keys. Show how Eve can do it to decrypt Bob’s ciphertext in the previous question. Demonstrate it using the following information:
[hint use the Genius gcd(nB,nE) function to find the common prime p, then calculate q, etc.] [12 marks]
Eve’s public key <e,n> components as follows;
public e = 7
modulus n =
d4a2038a1a7c14f55e65bc16939df3012a522e810e42d3aabdd75233e7cce7d3d63a3e1c9b987a33e1d1711ed20a494659400ecf3e568ef8450660a2e062350d149043ab29d50ba248807a97be6a0c6aa15cc8dd3915814ef0ca2db359e47f8599d97c0c33f39a92b1e29ec9fd2101552d60cf6fc74da90788d8257ee1d77aeb
Eve obtains Alice’s public key <e, n>.
e = 7;
modulus n = cba9710876d6026eac1a495399a941ca2a508bd85d4a6070062ec35d47e43f75c0060e0b57a8308b39b0736f72cc281716d278196d4c881d9dee2e545f21a607d406a1d2f182a7f39d7878a556c0146db12e2219feef9b0ddfce9d90bc87a5eb3be00dcd68b520d601c52cb545866d4d2edbfb3d26a8d2713dba41324704e0d9
Show that if Oscar and Alice shares a common prime, Oscar can calculate Alice’s private keys and Bob’s ciphertext C above, can decrypt the message meant for Alice.
Question 5. Breaking RSA by factorization Cryptography代写
Alice wants to obtain Bob’s PIN for his bank account. She sends Bob her public key <e, n> where e=7, n = 180276203. Bob encrypt the PIN and sends to Alice the ciphertext C = 165531788
Oscar monitors the transmissions and was able to obtain all the messages. Show how Oscar, by factorizing n, can obtain the PIN. [10 marks]
Question 6. Diffie Hellman key exchange
Alice and Bob wish to exchange a secret session key using the DH algorithm. They agree to use the global parameters: G = 3; p = 10061
a) Demonstrate, showing the computations and exchanges, how they can use the DH key exchange scheme to obtain a shared session key. (12 marks)
b). Would any party, Alice or Bob be able to control what the session key should be? (2 marks)
c). Suppose Oscar manage to steal the session key Ks1 from Alice which she already used to encrypt 100 messages. Oscar can decrypt all those messages. However, for the next 100 messages, Alice and Bob decide to derive a new session key;
(i) by hashing the current session key using MD5, i.e.
Ks2 =Hash(Ks1)
Would Oscar be able to obtain the new session key Ks2? (2 marks)
(ii) by carrrying out the DH key exchange again to obtain a new session key. If the Oscar cannot break the DH algorithm, can he obtain the session key? (2 marks)
Explain what is perfect forward secrecy and how this can be achieved. (2 marks)
[20 marks]
Question 7. ECDH key exchange Cryptography代写
Alice and Bob wish to exchange a secret session key. They decide to use the prime192v1 elliptic curve which generates 192 bit keys.
Openssl tools for ECDH
- Generate private key using the prime192v1 elliptic curve.
openssl genpkey -algorithm EC -out BobPrvkey.pem -pkeyopt ec_paramgen_curve:prime192v1
- Displa
openssl ec -in myPrvkey.pem -text -noout
- Extract public key
openssl ec -in myPrvkey.pem -pubout -out myPubkey.pem
- Derive a shared secret key
openssl pkeyutl -derive -inkey myPrvkey.pem -peerkey hisPubkey.pem -out mySecret
Paste screen shots of the steps and results:
a). Alice and Bob generate their private keys. Give suitable names to clearly distinguish them. Display their private keys. (4 marks)
The private key actuall contains both the private and public keys. How may bits is the private key? (1 mark)
The public key starts with a 04 (hex) indicating uncompressed format. Excluding this byte, how many bits is the public key? (1 mark)
b). Extract their public keys and display. How many bits are they. (4 marks)
b) Derive a secret key using each others public key with own private key. Name them differently for comparison. (6 marks)
c) Display both secret keys using hexdump, hexcurse, or xxd. Are they the same? How many bits is this key. (4 marks)
[20 marks]




