Heteroskedasticity代写
Lecture 3: Test for Heteroskedasticity
Heteroskedasticity代写 In Lecture one, we have learned that one of the assumptions of OLS regression is variance of the unobserved…
-
What is heterskedasticity? Heteroskedasticity代写
In Lecture one, we have learned that one of the assumptions of OLS regression is variance of the unobserved error terms, conditional on the explanatory variables, being constant, i.e., 
(Note 
is constant).
Homoskedasticity fails whenever the variance of the error terms changes across different segments of the population, where the segments are determined by the different values of the explanatory variables, i.e.,
-
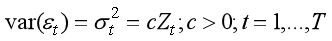
Consequences of heteroskedasticity for OLS
Heteroskedasticity does not cause bias or inconsistency in the OLS estimates.
The interpretation of our goodness-of-fit, R_square, is also unaffected by the presence of heteroskedasticity.
However, the estimators of the variance are biased without the homoskedasticity assumption. The usual OLS t-statistics do not have t-distributions in the presence of heteroskedasticity and the problem is not resolved by using large sample size.
-
Testing for heteroskedasticity Heteroskedasticity代写
Over the years, many possible approaches have been suggested, such as Goldfeld-Quandt test, Breusch-Pagan test, and White test etc..
We will restrict ourselves to more modern test, i.e., regessions using squared residuals.
The idea of testing for heteroskedasticy is based on the use of squared OLS residuals as a proxy for unobservable squared disturbances using the following specification
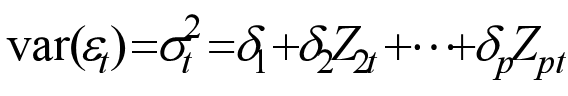
Z can be any variable that is included in the explanatory variables X, or a transformation of such variables, or a new variable that does not appear in X.
In principle, the parameters
….
can be estimated from a regression of 
on Z. If the squared OLS regressed on Z, we obtain an estimated model, which can be written as
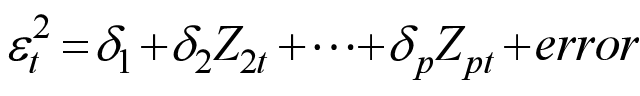
If the parameters 
….are all zero, variance is a constant, equal to and there is no heteroskedasticity in the error terms to the original model.
This suggests that one can test the null hypothesis of no heterodskedasticity by testing
We can use a large sample of test:
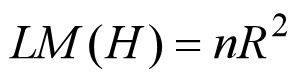
Under the null hypothesis, 
is approximately 
with (p-1) degrees of freedom. So if the value of nR2 is greater than 5% critical value for a distribution 
with p-1 degrees of freedom, the null hypothesis of no heteroskedasticity is rejected at 5%significant level.
-
How to conduct the estimation in the presence of heteroskedasticty?
Feasible GLS (FGLS)
