APM462: Homework 5
Comprehensive assignment for fifirst term
Machine Learning作业代写 This is question about optimization with inequality constraints. The problem we will investigate arrises in the…
(1) This is question about optimization with inequality constraints. The problem we will investigate arrises in the context of Support Vector Machines which is a fifield of Machine Learning. You do not need to know any machine learning to solve this problem, but here is some discussion in case you are intereted. If you wish, you can ignore the discussion and go directly to the details of the problem. Machine Learning作业代写
Suppose you are given m points xi ∈ Rn, i = 1, . . . , m (these points are called ‘data points’). Each point xi is labeled by a number yi which is either +1 or −1. You can think of the data {(xi , yi) | i = 1, . . . , m} as a collection of points in Rn some of which are labeled + and some labeled −. The goal is to separate the + points from the − points by a hyperplane. In general this may not be possible, but here we assume that it is possible to separate the + points from the − points by a hyperplane. For example, in one application the + data points label pictures of dogs, and the − data points label pictures of cats, and we would like to fifind an affiffiffine function that can tell the difffference between these cats and dogs, which is equivalent to fifinding a separating hyperplane.
Recall that any hyperplane in Rn can be specifified by a vector w ∈ Rn and a number b: {x ∈ Rn | w · x + b = 0}. Note that the hyperplanes separating the + points from the − points are the ones satisfying: yi(w · xi + b) ≥ 0 for all i = 1, . . . , m. For any such separating hyperplane (w, b), the distance to the closest data point is given by:
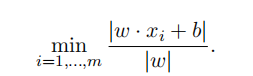
When building a SVM people want to pick, among all the many separating hyperplanes, one that is optimal in the following sense:
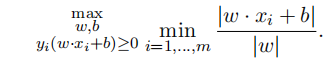
The solution to this optimization problem is a hyperplane that maximizes the distance to the closest datapoint, which is the most “stable” separating hyperplane. For example, if you choose a hyperplane that is very close to one of the data points, then a new nearby datapoint of the same class might be misclassifified by your SVM in the future, which is something you would like to avoid.
It is not diffiffifficult to show that the above problem is equivalent to the following problem, which is the problem (*) we will be investigating in this question:
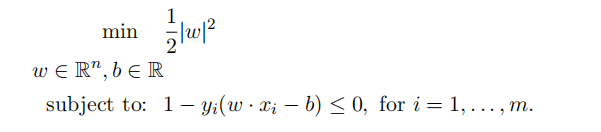
(a) Write the 1st order conditions for the problem (*) above. Note that the unknowns here are the vector w ∈ Rn and the number b ∈ R. Use µi as Lagrange multipliers.
(b) Suppose the data you are given has only two points x1 and x2 where y1 = +1 and y2 = −1. Use your conditions from part (a) to fifind a candidate for the optimal separating hyperplane for the two points x1 and x2. Hint: your answer should be a vector w and a number b expressed in terms of of the points x1 and x2. Machine Learning作业代写
(2) This question is about the meaning of Lagrange multipliers. Let F, g : R3 → R be two C1 functions and let S := {x ∈ R3 | g(x) = 0} 6= ∅ be the surface defifined by g. Assume S is a regular surface, that is every point of S is a regular point. At every point p ∈ S defifine the vector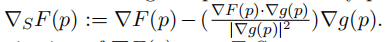 
Note that ∇SF(p) is the projection of ∇F(p) onto TpS.
(3) Referring to the notation in question (2) above, let g(x, y, z) = x2 + y2 + z2 − 1 and F(x, y, z) = −z be two C1 functions on R3. Compute ∇SF and fifind all the points p ∈ S where ∇SF(p) = 0.
(4) Recall that in lecture I proved that at a regular point p, TpM ⊆ Tp and then said that equality follows from the Implicit Function Theorem. In this problem you are asked to prove Tp ⊆ TpM in a special case.
Let f : Rn → R be a C1 function. Recall from HW4 that the graph of f is the surface M := {(x, f(x)) ∈ Rn × R | x ∈ Rn} in Rn × R. Machine Learning作业代写
(a) Let p := (x0, f(x0)) ∈ M. Find the space Tp.
(b) Show that Tp ⊆ TpM. That is show that any vector in the space Tp is a tangent vector to M at p. Note: unlike the case on HW4 Q7, here you are not allowed to assume that Tp = TpM.
(5) Let f : R3 → R, and g : R2 → R1 be C1 functions. Use Lagrange multipliers (1st order conditions) to show that fifirst constrained optimization problem. And the second unconstrained problem have the same candidates for minimizers:
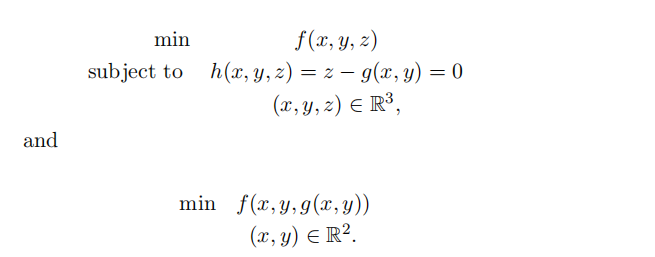
Note: the fifirst problem involves the variables x, y, z while the second one only x, y.
(6) Let Q be a 2 × 2 positive defifinite symmetric matrix. Let f ∈ C2 be an increasing, non-negative, and convex function on R1 . Let F(s) denote the area of the sublevel sets {xTQx ≤ f(s)2}: Machine Learning作业代写
F(s) = area {x ∈ R2 | xTQx ≤ f(s)2}.
Prove that the function F(s) is convex.
(7) Let R > 0 and assume the following problem has a solution:
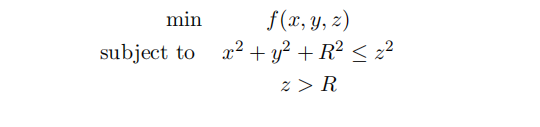
Note that the Kuhn-Tucker conditions (*) are:
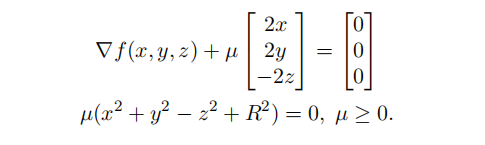
(a) Write the Kuhn-Tucker conditions for the following problem using Lagrange multipliers µ1 and µ2: Machine Learning作业代写
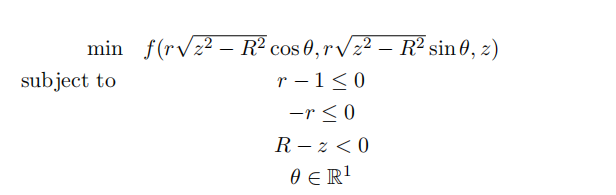
(b) Show that the conditions you found in part (a) for a point (r, θ, z) imply the Kuhn-Tucker conditions (*) for the corresponding point (x, y, z) = (r√z2 − R2cos θ, r√z2 − R2 sin θ, z).Start by expressing µ in terms of µ1 and µ2. There should be three cases to consider: when r = 0, 0 < r < 1, and r = 1.
