Relativity – basic effects
physical代考 Anneis in a train car (length L’) moving with speed v past Bob, who stands alongside the Anne shoots a photon from the back…
- Anneis in a train car (length L’) moving with speed v past Bob, who stands alongside the Anne shoots a photon from the back of the car to the front, where the photon bounces off a mirror, returning to Anne.
a. How much time does the photon’s round trip take in Anne’s frame?
b.How much time does the photon’s trip take in Bob’s frame?
a) The photon takes a time L’/c to reach the end, and then L’/c to Total time is 2L’/c physical代考
b) Since the two events in Anne’s frame (photon leaves, photon returns) occur at the same place in Anne’s frame, the duration for her is simply time-dilated by the factor γv. Thus for Bob the time is 2γvL’/c
-
Anneis in a train car (length L’) moving with speed v past Bob, who stands alongside the Anne has two synchronized clocks at the front and back of the train. At the moment both clocks read 12:00 they cause marks to be stamped on the ground. How far apart are the marks in Bob’s frame?
For Anna the two events occur at the same time, a distance L’ apart. In her frame, the ground is length-contracted by a factor γv. Therefore the distance between the marks in Bob’s frame is γvL’
- Anne isin a train car (length L for her) moving to the east with speed v=0.8c (relative to the ground) and Bob is in a train car (also length L for him) moving to the west with speed 8c.
a.With what speed does Bob see Anne’s car moving? physical代考
b.How long does it take Anne’s car to move completely past Bob’s car, according to Bob? (That is, the time from when the front of each car passes to the time the rear of each car )
a) Using the addition of velocities formula we have that the speed of Anna’s car is vrel = (0.8+0.8)c/(1+0.8×0.8) = 6c/1.64= 0.9756c
b) Bob sees Anna’s car has a length L/γ. Once the front end of Anna’s car reaches the front end of Bob’s, Anna’s car takes a time L/γvrel for its back end to reach the front of Bob’s Then the back end of Anna’s car takes a time L/vrel to reach the back of Bob’s car. Thus the total time is L/vrel(1+1/γ)
Relativity – kinematics physical代考
- Aparticle of mass M decays from rest to a photon and a particle of mass Find the momentum of the photon in the decaying particle reference frame.
The photon and the particle of mass m have equal and opposite momentum, p. The initial total energy is equal to the final total energy:
Mc2 = pc + (p2c2 + m2c4)1/2
Squaring both sides, and solving for the momentum we find
p = (M2 – m2)c/2M physical代考
- Aproton (mass m) with momentum p strikes another proton at The collision results in a new particle of mass 3m. What was the momentum of the original proton?
The initial and final total momentum remains p. Thus our expression for the initial and final total energy is
(p2c2 + m2c4)1/2 + mc2 = (p2c2 + (3m)2c4)1/2
After some algebra we find
p = 3√5/2 mc
-
Aparticle of mass M decays to three particles each of mass m < M/3. The momenta of the three particles are all equal, and they fly off at angles 120 degrees to each other. What is the momentum of each decay particle?
From conservation of energy, and seeing that all three particles have the same momentum p, we can write
Mc2 = 3 (p2c2 + m2c4)1/2
M2c4 = 9(p2c2 + m2c4)1
p2 = (M2/9 – m2)c2
Wave/particle duality and photons physical代考
- In a photoelectric effect experiment, in which an aluminum plate is exposed to 240 nm UV radiation, electrons are observed to be ejected from the If the work function of aluminum is 4.08 eV, what is the kinetic energy of the ejected electrons?
The photon energy is (1240 eV nm)/(240 nm) = 5.166 eV
There fore the electrons are ejected with (5.166-4.08) eV = 1.0867 eV
-
An electron beam with 100 eV kinetic energy electrons shines on the surface of a metal whose atomic planes are 2 nm apart. At what angle θ from the surface of the metal will one observe the first maximum in the reflected electron intensity (where the outgoing reflected beam makes the same angle θ with the surface)?
The wavelength of the 100 eV electrons is given by
λ = h/p = (hc)/(pc) = (hc)/√(2mc2K) = (!240 eV nm)/(2(511k)(100))1/2 = 0.123 nm
Using the Bragg diffraction formula
2d sinθ = nλ → sinθ = (0.123 nm)/2(1.2 nm) = 0.051 so θ = 2.9o

Bohr model physical代考
- An electron in a hydrogen atom decays from the n=4 to the n=2 state, emitting what wavelength photon?
The photon energy is given by (13.6 eV)(1/4 – 1/16) = 2.55 eV
The wavelength is therefore 486.3 nm
- What is the ground state energy of the He+ ion?
The expression for the hydrogen ground state energy depends on the proton charge squared, so the ground state energy og He+ is four times deeper, or -54.4 eV
Bohr model physical代考
- An electron in a hydrogen atom decays from the n=4 to the n=2 state, emitting whatwavelength photon?
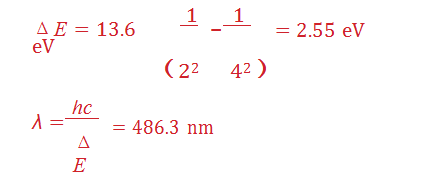
Schrodinger equation – bound states
- An electron is confined to a one-dimensional nanowire of length 100 nm. What is theenergy of the electron, in eV, if it in the first excited state?
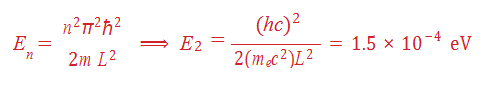
- What is the uncertainty in the momentum Δp of the electron in the previousproblem? (Just use the length of the nanowire as the uncertainty in position…)
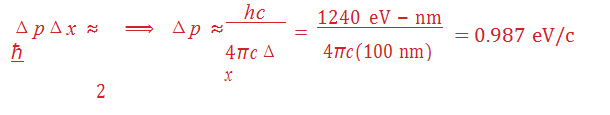
- AnO2 molecule is in the first excited vibrational The mass m of each oxygen atom is 1.336×10-26 kg, and the effective spring constant of O2 is κ = 1133 N/m. If the molecule decays to the ground state, what is the photon wavelength emitted? (Remember to use the reduced mass m/2.)
The energy difference between adjacent quantum harmonic oscillator states is given by
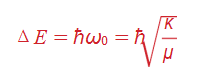
where the reduced mass μ = m/2. Plugging in we find ΔE = 0.2715 eV
Schrodinger equations – unbound states physical代考
- Abeam of electrons with kinetic energy 100 eV in a potential free zone ancounters a region where the potential changes by +50 eV. What fraction of the electrons are reflected from the barrier?
Using eq. 6-7 we have
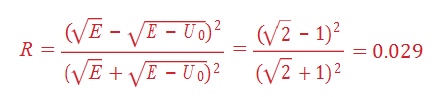
- An electron with 50 eV of kinetic energy encounters a potential barrier of 60 eVheight and 0.1 nm width. If the electron tunnels through the barrier whhat is its kinetic energy on the other side? physical代考
The kinetic energy on the far side of the barrier is the same as the kinetic energy before the barrier, 50 eV




