Homework 4
PMATH作业代写 Problem 1 (An alternative formulation of quadratic reciprocity). For an odd prime p, defifine
Show that quadratic reciprocity is…
1 More on Quadratic Residues PMATH作业代写
Problem 1 (An alternative formulation of quadratic reciprocity). For an odd prime p, defifine 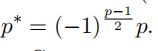Show that quadratic reciprocity is equivalent to 
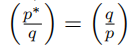for odd primes p and q. Can you extend this to Jacobi reciprocity?
A lot of proofs of quadratic reciprocity actually prove the statement above as opposed to the more “symmetric” statement that you read in the book.
Problem 2. Let p be an odd prime, and let a ∈ Z such that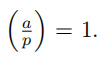 
Show that a is a square (mod pn ) for all n ≥ 1.
Can you come up with a necessary and suffiffifficient condition for an odd integer to be a square (mod 2n ) for all n? PMATH作业代写
Problem 3. Let s2(n) be the number of ways to write n as the sum of two squares. Show the following:
- If p is a prime that is congruent to 1 (mod 4), then s2(pn ) = 4(n + 1).
- If p is a prime that is congruent to 3 (mod 4), then s2(p2n ) = 4 and s2(p2n+1) = 0.
- s2(2n ) = 4.
- If a and b are coprime, then s2(a)s2(b) = 4s2(ab).
This lets one compute s2(n) for all n.
2 The Squareroot Algorithm PMATH作业代写
Problem 4. Let p ≡ 3 (mod 4), and a a quadratic residue in Z/pZ . Explicitly construct a number b such that b2 = a.
Problem 5. This gives the squareroot algorithm in full detail, and keeps notation as above (p, n, m, ζ).
(a) Let a be a quadratic residue. Explicitly construct an n-almost squareroot of a.
(b) Assume that a is a quadratic residue, and bk is a k-almost squareroot with 1 < k ≤ n. Show that you can multiply bk by a computable power of ζ to construct a (k −1)-almost squareroot of a, called bk−1.
This gives the algorithm: fifind ζ, then fifind bn, then iteratively fifind bn−1, bn−2, . . . , b2, and b1, which is an actual squareroot of a.
Problem 6. Use this algorithm to fifind a squareroot of 2 (mod 4001). If you need an example of such a ζ, notice that −3 is a quadratic non-residue and (−3)125 ≡ 662 (mod 125). PMATH作业代写
