Regression model代写
Lecture 4: Test for Structural Break
Regression model代写 A classic problem in econometrics is determining whether the coefficients of a regression model are the same…
A classic problem in econometrics is determining whether the coefficients of a regression model are the same in two separate subsamples.
In the case of time-series data, the subsamples would normally correspond to different time periods, and these tests are referred to as tests for Structural Break.
Sometimes we may be interested in testing whether the coefficients are the same in two different time periods. In such cases, time series data sets may be divided into earlier and later periods in a fairly arbitrary way for purposes of testing. This is legitimate, but such tests are more interesting when there is reason to believe that the subsamples correspond to different economic environments, such as different exchange-rate or policy regimes.
The classic test for equality of two sets of coefficients in linear regression models is called Chow test.
The standard way is to partition the data into two parts, the n-vector of y of observations on the dependent variable being divided into two vectors 
and 
of length 
and 
respectively, and the 
matrix of X of independent variables being divided into two matrices 
and 
of dimension 
and 
, respectively. Thus,
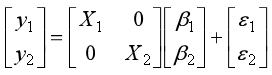
Where 
are the parameters to be estimated. The null hypothesis to be tested is that 
. Under the null hypothesis Equation (1) reduces to
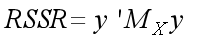
It is easy to construct a test of (1) against (2) by using the ordinary F test. The unrestricted sum of squared residuals from estimation (1) is
Where
. The restricted sum of squared residuals from estimation (2) is
Thus the ordinary F statistics is
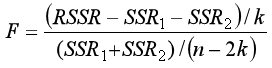
This test has k and n-2k degrees of freedom.
