STA305/1004 – L0101 Term Test 1 SOLUTION GUIDE
Stata作业代写 Instructions: Answer all four questions in the space provided within 90 minutes. Work written on the back of pages will…
Instructions: Answer all four questions in the space provided within 90 minutes. Work written on the back of pages will not be graded.
Aids allowed: One 8.5’x11’ sheet with writing on both sides, and a non-programmable calculator. The table below shows the value of each question.
This test contains 18 pages including this page. Stata作业代写
- (30 marks) (Adapted from Box, Hunter and Hunter) Ten hens were randomly allocated to two differentdiets, A or B. Five were assigned to Diet A and five to Diet B. After one year the number of eggs produced are given in the table The hens are identified by the number in parentheses.
Diet A 166 (1) 174 (2) 150 (3) 166 (4) 165 (5)
Diet B 158 (6) 159 (7) 142 (8) 163 (9) 161 (10)
The randomization distribution and related output for testing H0 : µA = µB versus H1 : µB < µA (there was a typo here!), where µA, µB are the mean number of eggs for diets A and B respectively, were calculated. Some of the R code is shown below.
yA <- c(166,174,150,166,165)
yB <- c(158,159,142,163,161)
eggs <- c(yA,yB) #pool data
for (i in 1:N)
{
res[i] <- mean(eggs[index[,i]])-mean(eggs[-index[,i]])
}
hist(res,xlab="meanA-meanB", main="Randomization Distribution of difference in means")
observed <- mean(yA)-mean(yB) #store observed mean difference
abline(v=observed) #add line at observed mean diff
Randomization Distribution of difference in means Stata作业代写
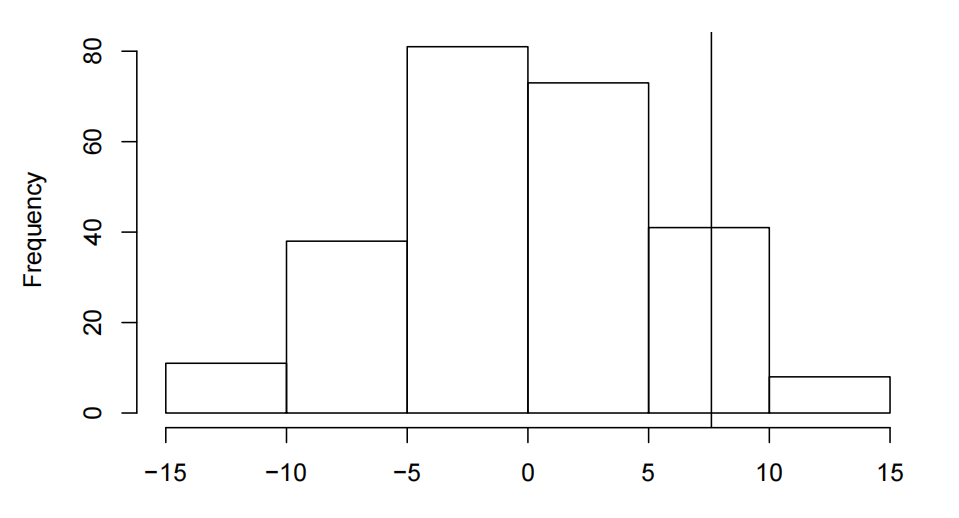
meanA−meanB
observed # Observed difference in means [1] 7.6 sum(res>=observed) [1] 30
Answer the following questions based on this study.
(a) (5marks) Is this study an experiment or observational study? Briefly explain your reasoning.
Experiment. The treatment assignment mechanism is known. In other words, the mechanism of how treatments were assigned to units is known.
(b) (5 marks) Give two examples of possible treatment assignment for this study under the nullhypothesis that are not the observed treatment assignment. Use the table below to fill in the treatment assigned to each Use A for diet A and B for diet B.
Any two treatment assignment that assigns 5 hens to diet A and 5 hens to diet B, besides the observed assignment.
| Hen | Treatment assignment #1 | Treatment assignment #2 |
| 1 | ||
| —— | ————————- | ————————- |
| 2 | ||
| —— | ————————- | ————————- |
| 3 | ||
| —— | ————————- | ————————- |
| 4 | ||
| —— | ————————- | ————————- |
| 5 | ||
| —— | ————————- | ————————- |
| 6 | ||
| —— | ————————- | ————————- |
| 7 | ||
| —— | ————————- | ————————- |
| 8 | ||
| —— | ————————- | ————————- |
| 9 | ||
| —— | ————————- | ————————- |
| 10 |
(c) (5marks) What is the propensity score in this study? What is the probability of treatment assignment? Is the treatment assignment ignorable? Briefly Stata作业代写
The propensity score is the probability of a hen is assigned, say, diet A = 5/10.
The probability of a treatment assignment is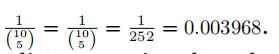 
The treatment assignment is ignorable since diet was assigned randomly and the hens’ eggs production should be independent of the diet assigned.
(d) (5marks) What is the p-value of the randomization test? Is there evidence at the 5% significance level that diet A is better than diet B? Briefly explain your reasoning.
The p-value is 30/252=0.119. The p-value > 0.05, therefore there is no evidence of a difference in egg production between the two diets A and B, at the 5% level.
(e) (10 marks) Suppose another investigator would used a different set of 10 hens to compare the 2diets, but would like to use a randomized paired design instead of the design described above. In one or two sentences describe how this study could have been designed as a randomized paired What are the treatments and experimental units? How would you randomize the treatments to the units? What is the propensity score and probability of treatment assignment in your paired design? Stata作业代写
The experimental units are the hens and the treatment is diet.
AND
Here are two possible ways to obtain a randomized paired design:
Answer 1
Pair the hens by a common covariate. Within each pair, randomly assign diets A and B. Here the propensity score is 1/2 and the probability of treatment assignment is 1 .
OR
Answer 2
Randomly assign one of the two diets to each hen, say for 12 months. After a wash-out period, offer the other diet to the same hen for another 12 months. For example, if a fair coin is tossed shows heads, then hen 1 is assigned to diet A for the first 12 months, then does diet B for 12 month after the wash-out period. Here the propensity score is 1/2 and the probability of treatment assignment is 1 .
-
(20marks) (Adapted from Box, Hunter and Hunter) Paint used for marking lanes on highways must be very durable. Double yellow lines are used to mark the centre of a road to separate lanes of traffic travelling in opposite directions. In one trial, yellow paint from two suppliers, labelled A and B,was randomly assigned to the two centre lines on six different highway sites, denoted 1, 2, 3, 4, 5, After a considerable length of time, the average wear for the samples at the six sites were as follows: Stata作业代写
| Site | Paint A | Paint B |
| 1 | 59 | 69 |
| 2 | 65 | 83 |
| 3 | 64 | 74 |
| 4 | 52 | 61 |
| 5 | 71 | 78 |
| 6 | 64 | 69 |
paintA <- c(59,65,64,52,71,64) paintB <- c(69,83,74,61,78,69)
#Two-sample t-test; equal variance t.test (paintA, paintB, paired=FALSE, var.equal=TRUE)
## ## Two Sample t-test ## ## data: paintA and paintB ## t = -2.3971, df = 10, p-value = 0.0375 ## alternative hypothesis: true difference in means is not equal to 0 ## 95 percent confidence interval: ## -18.9735320 -0.6931347 ## sample estimates: ## mean of x mean of y ## 62.50000 72.33333
#Two-sample t-test; unequal variance t.test (paintA, paintB, paired=FALSE, var.equal=FALSE)
## ## Welch Two Sample t-test ## ## data: paintA and paintB ## t = -2.3971, df = 9.6661, p-value = 0.0383 ## alternative hypothesis: true difference in means is not equal to 0 ## 95 percent confidence interval: ## -19.0165158 -0.6501509 ## sample estimates: ## mean of x mean of y ## 62.50000 72.33333
## ## Paired t-test ## ## data: paintA and paintB ## t = -5.4176, df = 5, p-value = 0.002901 ## alternative hypothesis: true difference in means is not equal to 0 ## 95 percent confidence interval: ## -14.499095 -5.167572 ## sample estimates: ## mean of the differences ## -9.833333
Normal Q−Q Plot for Paint A
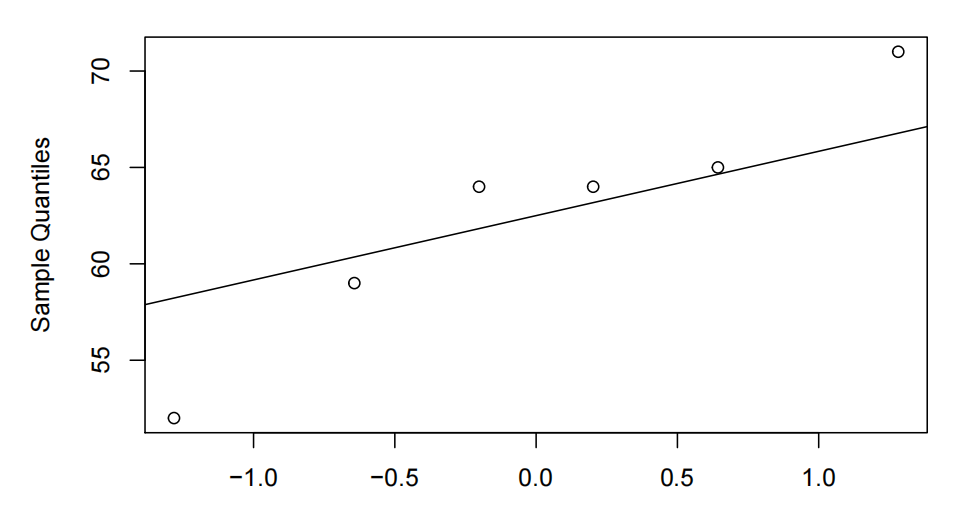
Theoretical Quantiles
Normal Q−Q Plot for Paint B
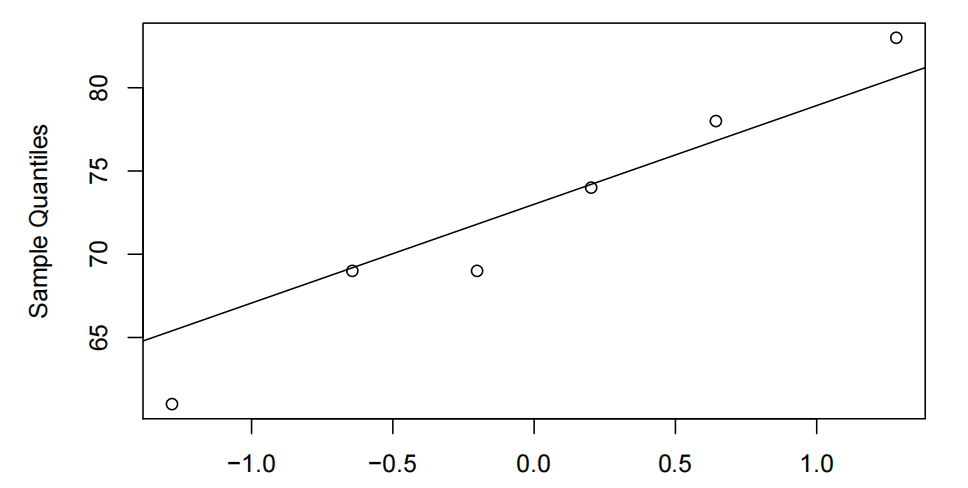
Theoretical Quantiles
Normal Q−Q Plot for Difference
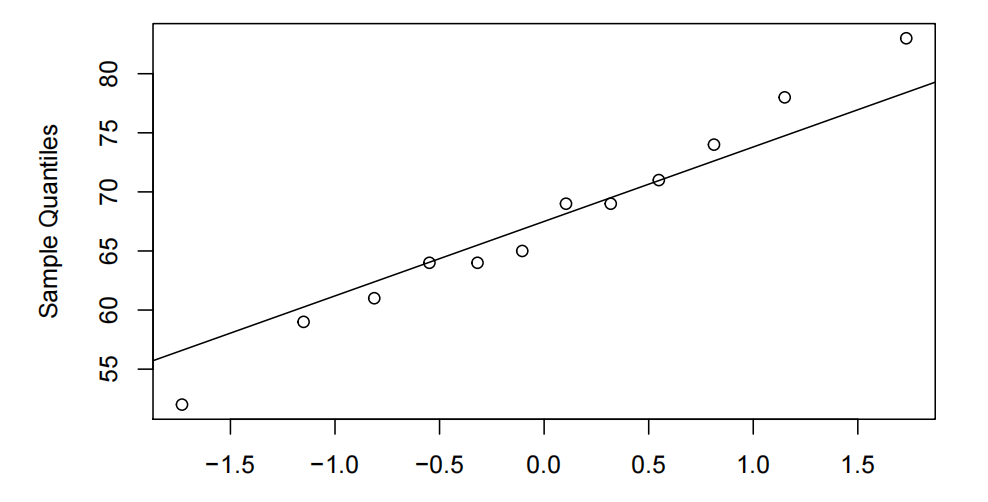
Theoretical Quantiles
(a) (5marks) What is the name of the study design? Justify your answer.
Randomized paired design. Paint was randomized within each site. Stata作业代写
(b) (5 marks) Is this studyan experiment or an observational study? Justify your answer.
An experiment since the treatment assignment mechanism was under the control of the researcher and the probability of treatment allocation was known before the experiment begun.
(c) (5marks) Is there a statistically significant difference between the mean wear of A and B at the 1% significance level? Justify your
Yes, since the p-value of 0.003 is less than 0.01.
(d) (5marks) Would it have been more appropriate to conduct a randomization test for this data? Justify your Stata作业代写
The Q-Q plot for the differences does not deviate too much from the straight line. Hence, the normality assumption is satisfied for the paired t-test. Hence, the paired t-test was appropriate for the data. A randomization test is an exact test that does not require the assumption of normality or independence. A randomization test would have produced similar results.
- (25 marks) A psychologist studying body language conducted an experiment on 20 subjects, and obtaineda significant result from a two-sided z-test (H0 : µ = 0 H1 : µ = 0). Let’s call this experiment #1. The observed value of the z statistic from your experiment is z = 2.2 so the p-value=0.028. In order to confirm the results the psychologist is planning to run the same experiment on an additional 10 subjects (i.e., the same experiment will be done on 10 different subjects). Let’s call this experiment #2.
The following percentiles from the N (0, 1) distribution might be required to carry out some of the calculations in the questions below.
| α | zα |
| 0.468 | 0.08 |
| 0.100 | 1.28 |
| 0.050 | 1.64 |
| 0.025 | 1.96 |
| 0.020 | 2.05 |
| 0.010 | 2.33 |
zα is the 100(1 − α)th percentile of the N (0, 1). For example, the 90th percentile is z0.10 = 1.28.
(a) (5 marks) Assume that the true mean in experiment #2 is the sample mean obtained in theexperiment #1. What is the probability that the results of experiment #2 will be significant at the 5% level by a one-tailed z-test (H1 : µ > 0)? Provide a brief interpretation of this probability. Stata作业代写
Assume 
Experiment #2 rejects when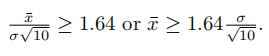 
Now standardize
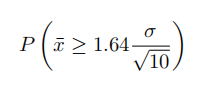
by subtracting µ and dividing by σ/√10. This gives,
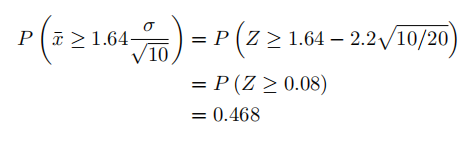
This means that the experiment has about 47% power.
(b) (10 marks) The psychologist strongly believes in her theory, and would like a sample size formulafor experiment #2 so she can calculate the sample size given α – type I error rate and β – type II error Derive such a sample size formula for the psychologist as a function of α, β and Φ ( ) the cumulative distribution function of the N (0, 1).
The test rejects when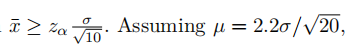 
the power of the test, 1 − β, can be
calculated as
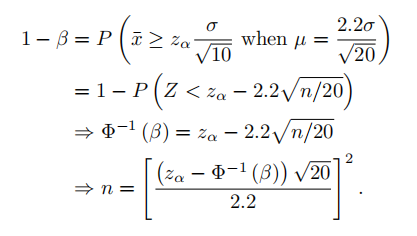
(c) (5marks) The power function derived in part (b) was used to create a plot of sample size n versus β, the probability of a type II error.
Sample size versus b for experiment #2
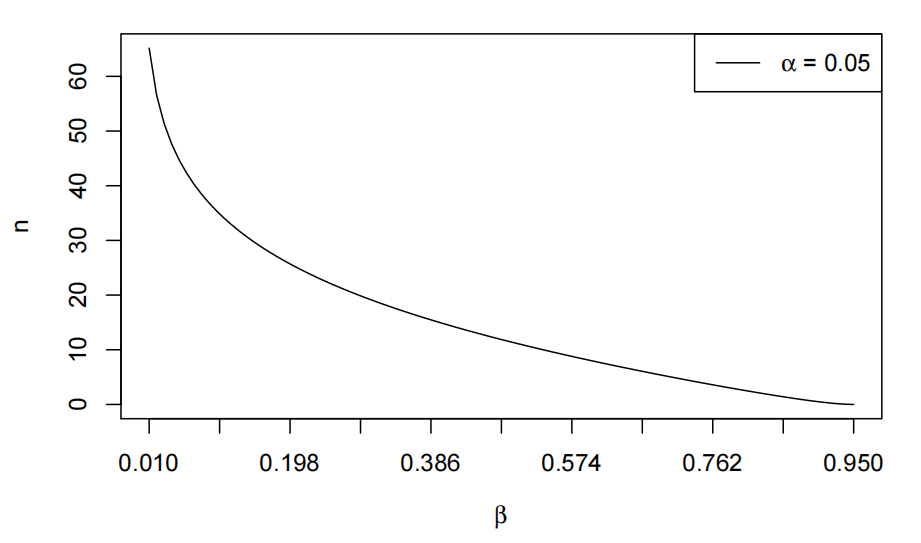
What does the plot tell you about the relationship between sample size and power for experiment #2? Use the plot to estimate how many subjects the psychologist would have to enrol so that experiment #2 will have 80% power at the 5% significance level. Should she revise her original design and enrol more than 10 subjects in experiment #2, if she want to be more confident of rejecting H0 when in fact µ > 0?
The plot shows that as β decreases n increases which implies that power increases as n increases.
From the plot n is approximately 25.
The psychologist should revise her original sample size of 10 to at least 25 since this would give her approximately 80% power.
(d) (5 marks) Suppose the psychologist decided to change the significance level in experiment #2 from5% to 10%. The plot of n versus β is shown for three values of α, the type I error rate, but the statistician that created the graph forgot to label two of the three curves in the plot. Should she use the curve above or below the curve where α = 0.05 to estimate the sample size? Estimate the sample size required for experiment #2 to have 80% power at the 10% significance Briefly explain.
Sample size versus b for experiment #2 Stata作业代写
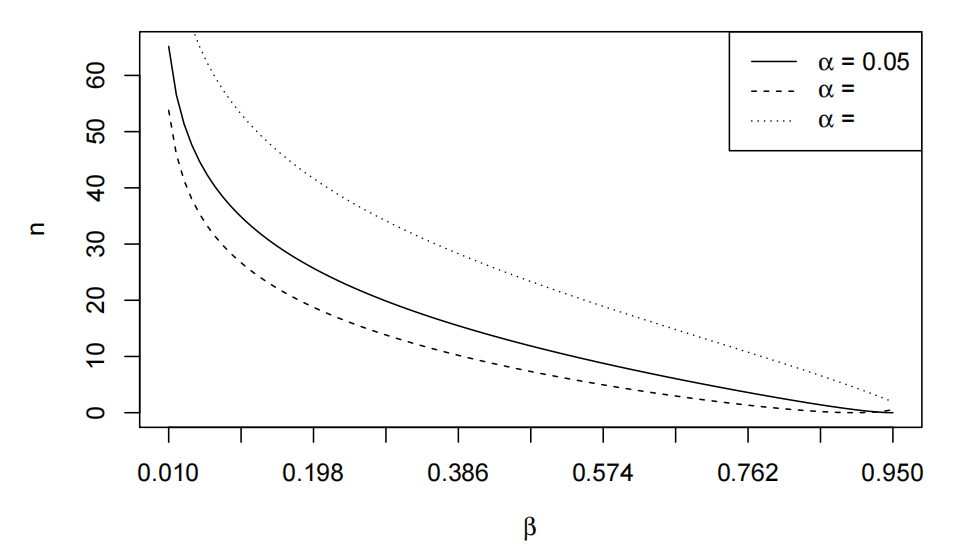
Using the power curve below α = 0.05 curve we have that n is approximately 20. The power curve below is used since as α increases n should decrease for a fixed value of β.
-
(25 marks) What is the effect of smoking on weight gain? Data was used from The National Healthand Nutrition Examination Survey Data I Epidemiological Follow-up Study (NHESFS) survey to assess this question. The NHESFS has information on sex, race, weight, height, education, alcohol use, and intensity of smoking at baseline (1971-75) and follow-up (1982) visits. The survey was designed to investigate the relationships between clinical, nutritional, and behavioural factors. A cohort of persons 25-74 who completed a medical exam in 1971-75 followed by a series of follow-up studies. Stata作业代写
The table below shows the distribution of the baseline covariates in the two groups. 403 people are in the smoking group (No cessation T=0) and 1163 people are in the smoking cessation group (T=1).
Cessation (T=1) No cessation (T=0)
| age, years (mean) | 46.2 | 42.8 |
| men, % | 54.6 | 46.6 |
| white, % | 91.1 | 85.4 |
| university, % | 15.4 | 9.9 |
| weight, kg (mean) | 72.4 | 70.3 |
| Cigarettes/day (mean) | 18.6 | 21.2 |
| year smoking (mean) | 26.0 | 24.1 |
| little/no exercise, % | 40.7 | 37.9 |
| inactive daily life, % | 11.2 | 8.9 |
The propensity score was estimated using a logistic regression based on all 9 covariates; no interactions were included in the propensity score model. Three propensity score methods were used to estimate the treatment effect (the average difference in weight gain between the smoking cessation group and the smoking group): propensity score matching, stratifying on the propensity score, regression adjustment using the propensity score, and no adjustment using the two-sample t-test. The propensity score methods successfully balanced all the covariates (i.e., the absolute standardized differences are less than 10%). The table below shows the average treatment effect for each method with the 95% confidence interval. The propensity score matching method was able to match the 403 subjects in the smoking group to 403 subjects in the smoking cessation group.
| Method | Average Treatment Effect | 95% Confidence Interval | |
| Matched | 2.93 | 1.8 – 4.0 | |
| Stratified | 3.26 | 1.7 – 3.4 | |
| Regression | 3.40 | 2.5 – 4.3 | |
| Unadjusted | 2.54 | 1.7 – 3.4 |
Answer the following questions. (5 marks each) Stata作业代写
(a) Is this an experiment or observational study? What is the treatment in this study? Briefly explain.
This is an observational study since the assignment mechanism (how subjects are assigned to the smoking or smoking cessation group) is unknown. The are two “treat- ments” in this study smoking and smoking cessation. In other words the treatment factor smoking has two levels: smoking; smoking cessation.
(b) Is the propensity score known or unknown in this study? Briefly describe how the propensity scorewas calculated for each subject. Give a formula showing how the propensity score is calculated and explain the terms in the
The propensity score is unknown since the probability of a subject being assigned to the smoking/smoking cessation group is unknown. The propensity score can be estimated from the logistic regression model by calculating the predicted probability of smoking for each subject.
(c) Briefly compare and contrast the methods of propensity score matching and stratification bypropensity
Matching involves finding pairs of treated and control units with similar propensity scores. It is not always possible to match every treated unit with a control unit. Hence, not all units may be used up in this method.
On the other hand, with stratification the whole sample is used up. Units are divided into groups based on similar propensity scores. Groups will contains more than 2 units. Stata作业代写
(d) In the context of this study briefly explain what it means for the treatment assignment to bestrongly Does this seem like a plausible assumption for this study?
The potential outcomes in this study are 1982 weight if the subject was a smoker and non-smoker, Y (1), Y (0), respectively. The treatment assignment, T , is smoking status. The treatment assignment is strongly ignorable if conditional on the propensity score smoking status is independent of the unobserved potential outcomes. This can be written symbolically as:
Y (0), Y (1)⊥T |e(x).
It seems plausible if the 9 covariates are all the important confounding covariates and no important covariates are missing. Conversely, it might not be plausible if at least one important covariate is missing. Stata作业代写
(e) For this study, is the treatment assignment unconfounded? Briefly explain.
Propensity score methods balance observed not unobserved covariates. If an im- portant covariate (confounder) is missing and is not balanced then it may lead to a difference between the treatment and control groups that is not due to treatment but due to the unobserved confounder. For observational studies, treatment assignment is not unconfounded.
更多代写：Jave代写 雅思代考 统计论文代写 经济学代写 数学代写 写作APP
