统计建模代写 因为污渍初始脏度要作为协变量,于是重新整合数据集,将全面相应变量拉到一个变量cleaning中,并对应在解释变量数据集中加入一个名义变量index。R-squared为0.8202,表示解释变量可以解释相应变量82.02%的信息。P-value小于0.05,因此回归方程的检验是显著的。

1、数据整理
因为污渍初始脏度(Baseline1-Baseline5)要作为协变量,于是重新整合数据集,将全面相应变量(Cleaning1-Cleaning5)拉到一个变量cleaning中,并对应在解释变量数据集中加入一个名义变量index。当index=1,对应Baseline1, Cleaning1;当index=2,对应Baseline2, Cleaning2;依此类推。另外将block, C1-C20, P1-P4复制4次,将250个样本数据拉到了1250个。
同时注意到,当固定block值,P2值为常值,故在接下来的建模过程中剔除这一变量。
2、统计建模
2.1 只考虑线性项 统计建模代写
lm(formula = cleaning ~ factor(block) + C1 + C2 + C3 + C4 + C5 + C6 + C7 + C8 + C9 + C10 + C11 + C12 + C13 + C14 + C15 + C16 + C17 + C18 + C19 + C20 + P1 + P3 + P4 + factor(index) + baseline, data = laundry) Residual standard error: 9.303 on 1159 degrees of freedom Multiple R-squared: 0.8202, Adjusted R-squared: 0.8062 F-statistic: 58.74 on 90 and 1159 DF, p-value: < 2.2e-16
R-squared为0.8202,表示解释变量可以解释相应变量82.02%的信息。P-value小于0.05,因此回归方程的检验是显著的。
2.2 考虑二次项和交叉项 统计建模代写
lm(formula = cleaning ~ factor(block) + C1 + C2 + C3 + C4 + C5 + C6 + C7 + C8 + C9 + C10 + C11 + C12 + C13 + C14 + C15 + C16 + C17 + C18 + C19 + C20 + P1 + P3 + P4 + factor(index) + baseline +C1^2 + C2^2 + C3^2 + C4^2 + C5^2 + C6^2 + C7^2 + C8^2 + C9^2 + C10^2 + C11^2 + C12^2 + C13^2 + C14^2 + C15^2 + C16^2 + C17^2 + C18^2 + C19^2 + C20^2 + P1^2 + P3^2 + P4^2 + C1 * P1 + C1 * P3 + C1 * P4 + C2 * P1 + C2 * P3 + C2 * P4 + C3 * P1 + C3 * P3 + C3 * P4 + C4 * P1 + C4 * P3 + C4 * P4 + C5 * P1 + C5 * P3 + C5 * P4 + C6 * P1 + C6 * P3 + C6 * P4 + C7 * P1 + C7 * P3 + C7 * P4 + C8 * P1 + C8 * P3 + C8 * P4 + C9 * P1 + C9 * P3 + C9 * P4 + C10 * P1 + C10 * P3 + C10 * P4 + C11 * P1 + C11 * P3 + C11 * P4 + C12 * P1 + C12 * P3 + C12 * P4 + C13 * P1 + C13 * P3 + C13 * P4 + C14 * P1 + C14 * P3 + C14 * P4 + C15 * P1 + C15 * P3 + C15 * P4 + C16 * P1 + C16 * P3 + C16 * P4 + C17 * P1 + C17 * P3 + C17 * P4 + C18 * P1 + C18 * P3 + C18 * P4 + C19 * P1 + C19 * P3 + C19 * P4 + C20 * P1 + C20 * P3 + C20 * P4, data = laundry) Residual standard error: 9.453 on 1099 degrees of freedom Multiple R-squared: 0.8239, Adjusted R-squared: 0.7999 F-statistic: 34.29 on 150 and 1099 DF, p-value: < 2.2e-16
在加入C1-C20, P1-P4的二次项及这两个类的交叉项后,发现Adjusted R-squared反而下降了,说明加了更多解释变量,对清洁能力的解释程度并没出现较大幅度上升。据此,最后我们不会考虑二次项和交叉项。
2.3 逐步回归 统计建模代写
考虑到(1)中有些回归系数不显著,因此我们通过逐步回归,以AIC信息统计量为准则,选择最小的AIC信息统计量来达到删除变量的目的。Step回归后的解释变量为:
cleaning ~ factor(block) + C1 + C6 + C13 + C14 + P1 + P4 + factor(index) C1 7.0379 0.7362 9.560 < 2e-16 *** C6 3.6791 0.8000 4.599 4.71e-06 *** C13 1.3765 0.7748 1.777 0.07589 . C14 1.1788 0.7462 1.580 0.11441 P1 -4.0575 0.7812 -5.194 2.43e-07 *** P4 6.1982 0.7479 8.288 3.12e-16 *** factor(index)2 -37.0104 0.8291 -44.640 < 2e-16 *** factor(index)3 9.6095 0.8291 11.590 < 2e-16 *** factor(index)4 3.8324 0.8291 4.622 4.21e-06 *** factor(index)5 -26.9762 0.8291 -32.537 < 2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 9.269 on 1177 degrees of freedom Multiple R-squared: 0.8187, Adjusted R-squared: 0.8076 F-statistic: 73.83 on 72 and 1177 DF, p-value: < 2.2e-16
回归系数检验的显著水平得到了很大的提高,但是C14的显著性检验仍没有通过,因此我们直接删除C14,并确定最后的预测模型。
2.4 最终模型 统计建模代写
Final model: cleaning ~ factor(block) + C1 + C6 + C13 + P1 + P4 + factor(index)
方差膨胀因子检验:
> vif(lm.final) GVIF Df GVIF^(1/(2*Df)) factor(block) 5.030919 62 1.013114 C1 1.357311 1 1.165037 C6 1.493310 1 1.222011 C13 1.340551 1 1.157822 P1 1.326220 1 1.151616 P4 1.430880 1 1.196194 factor(index) 1.000000 4 1.000000
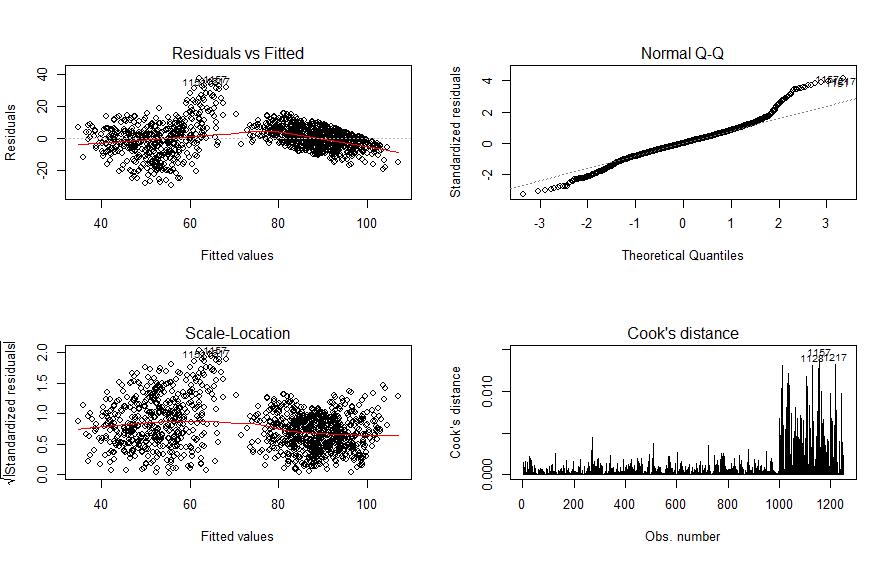
因为每个GVIF^(1/(2*Df))均小于10,所以可以判定不存在多重共线性。下图左上角为残差散点图,右上角为Q-Q Plot,左下角为标准化残差绝对值的开方的残差图,右下角为Cook距离图。
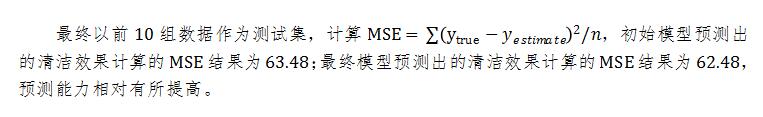
更多其他:Proposal代写 Academic代写 Essay代写 艾莎代写 Review代写 研究论文代写 Case study代写 Home Top Writers Blogs Login 文学论文代写 Report代写 ORDER NOW Admission




您必须登录才能发表评论。