代考数学final Math/STAT 4540/5540 – Final 

Math/STAT 4540/5540 – Final 

代考数学final You may discuss your work ONLY WITH ME. Send me an e-mail with possible times, and I’ll send you a zoom link.

Rules: 代考数学final

1. You may discuss your work ONLY WITH ME. Send me an e-mail with possible times, and I’ll send you a zoom link.

2. You don’t have to re-establish any formulas from the text or from homework solutions, but you have to state which formula is used.

3. You have to show ALL WORK.
4. All graphs should be computer-generated, not hand-sketched. Check the solutions to the homework if you are not sure what kind of graph is needed.

5. No matter what kind of software you are using (Excel, R, Matlab, etc.) and what you post on Canvas, you have to E-MAIL ALL the source FILES to me. 代考数学final

6. Each problem is worth 10 points except the bonus which is 5 points.

7. 5540 part will be posted as a separate assignment. 
8. For a given data set, fifit a linear trend, test the hypothesis H0 : b = 0 at the 5% level of signifificance, and construct a forecast with 95% confifidence bounds, for the next fifive values of the series. Graph the data together with estimated trend, prediction and confifidence bounds.

2. Apply the 53X procedure to a given data set, graph the data and the result.
3. Construct 5 steps ahead predictions for the data using exponential smoothing of the orders 0,1 and 2 (set the smoothing parameter α to 0.1). Graph the results. 代考数学final

4. Test if the data contains trend, using (a) Spearman rank correlation test; (b) Kendall rank correlation test. Use 5% level of signifificance.

5. Let Xt be a stationary series with autocovariance function RX(k). A new series Yt is defifined by the formula Yt = Xt − 2Xt−1 + Xt−2. Show that Yt is stationary. Express its autocovariance function RY in terms of RX.

6. Verify that the equation 代考数学final

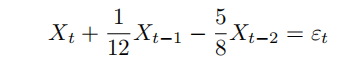
describes a stationary series. Find a formula for its ACF. Find its PACF. Find its spectral density, make a graph (assume σε2 = 1).

7. Do the following equations describe an ARMA(k, l) process (in particular, do they satisfy the stationarity and invertibility condition)? If yes, what are k, l? Do they describe an ARIMA(k, d, l) process? If yes, what are k, d, l?代考数学final

(a) Xt + Xt−1 − 0.5Xt−2 = εt − 1.5εt−1 + εt−2

(b) (1 − B + 0.75B2)Xt = (1 + B + 0.25B2)εt

(c) Xt − 0.2Xt−1 − 0.8Xt−2 = εt + 0.9εt−1

(d) Xt − 1.5Xt−1 − 0.15Xt−2 = εt + εt−1 − εt−2

8. For a data set, estimate the mean, the variance, fifirst 25 values of ACF and fifirst three values of PACF. Estimate the spectral density using triangular window with M = 25. Graph the result. 代考数学final
9. Find a formula, and graph the transfer function of the following fifilter:

Yt − 1.50462Yt−1 + 0.854081Yt−2 = 0.0729597(Xt − Xt−2).

What kind of fifilter is it?

10. Design a second order band pass tangent fifilter with cut-offff points 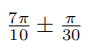and apply it to the data. Graph the results.

11. Bonus (5 points only). Find a formula for an ACF of an ARMA(1,2) process defifined by the equation 代考数学final

Xt + 0.9Xt−1 = εt − εt−1 + 0.25εt−2