Question
北美homework代写 A scientist conducts 1000 trials of an experiment involving variables X,Y, each with possible values {0, 1}. He records the…
SECTION A. 北美homework代写
Answer each of the following questions [ Marks per questions as shown; 25% total ]
- (8 pts) A scientist conducts 1000 trials of an experiment involving variables X,Y, each with possible values {0, 1}. He records the outcomes of the trials in the following table.

Compute each of the following, showing all your working.
(a) (1 pt) p(X = 1,Y = 1).
(b) (2 pt) p(X = 1).
(c) (1 pt) E[X].
(d) (2 pt) p(Y = 1|X = 1).
(e) (2 pt) p(X + Y = 1).
- (9 pts) Lorelai is taking an exam that involves multiple choice questions, with available choices {1, 2, . . ., c}, where c ≥ 2. For each question, there is only one correct answer, and Lorelai is allowed to provide only one choice as her answer. With 90% probability, Lorelai knows the answer for a question. When Lorelai knows the answer for a question, she always picks the correct choice. When Lorelai does not know the answer for a question, she makes a guess. When making a guess, Lorelai is equally likely to pick any of the c available choices.
(a) (2 pt) Show that the probability Lorelai does not know the answer for a question and guesses the correct answer is 北美homework代写
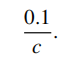
(b) (2 pt) Show that the probability Lorelai answers a question correctly is
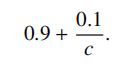
(c) (3 pt) Suppose Lorelai answers a question correctly. Show that the probability she knew the answer is
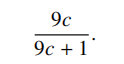
(d) (2 pt) When c gets larger, does the probability in part (c) get larger or smaller? Explain your answer intuitively in one or two sentences.
- (8 pts)
(a) (2 pt) In one or two sentences, explain what the likelihood function for a parameter is.
(b) (2 pt) In one or two sentences, explain what the maximum likelihood estimate for a parameter is.
(c) (2 pt) Suppose we have a coin which comes up heads with unknown probability p. We perform 5 independent flflips of the coin, and observe the outcomes
{heads, heads, tails, heads, heads}.
Based on this data, what is the maximum likelihood estimate for the probability p?
(d) (2 pt) Suppose our prior belief in the coin coming up heads follows a Beta(a, b) distribution for certain constants a, b. In one or two sentences, describe a procedure which can additionally incorporate this prior belief to estimate the probability p. (You do not need to compute the estimate for p using this procedure.)
Answer each of the following questions [ Marks per questions as shown; 25% total ] 北美homework代写
- (9 pts) Suppose X represents whether it is sunny or cloudy in Canberra, and Y represents whether it is warm or humid in Canberra. The joint distribution p(X,Y) is
p(X = sunny,Y = warm) = 1/2
p(X = sunny,Y = humid) = 1/4
p(X = cloudy,Y = warm) = 1/4
p(X = cloudy,Y = humid) = 0.
(a) (2 pt) In one or two sentences, explain what the entropy of a random variable represents.
(b) (3 pt) Compute the entropy H(X).
(c) (2 pt) Compute the joint entropy H(X,Y).
(d) (2 pt) Compute the conditional entropy H(Y |X).
-
(12 pts) Let X and Y be independent random variables with possible outcomes {0, 1}, with
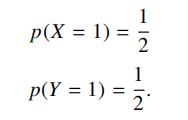
Let Z = X + Y.
(a) (1 pt) Compute I(X;Y).
(b) (4 pt) Show that
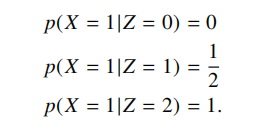
(c) (3 pt) Compute H(X|Z).
(d) (2 pt) Compute I(X; Z).
(e) (2 pt) Explain why parts (a) and (d) do not contradict the data-processing inequality.
- (4 pts) Dr. Seuss has set an exam for his class, where the possible scores are {0, 1, 2, . . ., 100} i.e. the exam is out of 100 marks. Dr. Seuss found that the average exam score of the students is 60 marks out of 100.

(a) (2 pt) What is an upper bound on the fraction of students who scored 80 or more in the exam? 北美homework代写
(b) (2 pt) Dr. Preibus has set an exam for a difffferent class, where the possible scores are {−100, −99, . . ., 99, 100} i.e. the exam is out of 100 marks, but it is possible to score negative marks. Dr. Preibus found that the average exam score of the students is 60 marks out of 100.
Is your answer from (a) also an upper bound on the fraction of students who scored 80 or more in Dr. Preibus’ exam? Explain why or why not.
7.(4 pts) Let X be an ensemble with AX = {a, b} and fifixed probabilities pX = (pa, pb).
(a) (2 pt) Conan has constructed a prefifix-free code C1 for X, with expected length L(C1, X). Is it possible that L(C1, X) < H(X)? Explain why or why not.
(b) (2 pt) Ronan has constructed a Huffffman code C2 for X. Is it possible that L(C2, X) > H(X)? Explain why or why not.
8.(5 pts) Suppose we wish to compress a string with LZ77 with a window size W = 2. Suppose we place two conditions on the string: it must have length 3 or more, and can only contain the symbols {a, b}. (For example, aba and bbb are valid strings, but ba (which has length 2) and abc (which contains the symbol c) are not.)
Recall that in LZ77, the output at any iteration is either of the type SYM (for an exact symbol match) or POINTER (for a window match).
(a) (2 pt) Give an example of a string satisfying the above conditions where, at every iteration of LZ77 except the fifirst, the output is of the type POINTER.
(b) (3 pt) Is it possible that for some string satisfying the above conditions, at every iteration of LZ77, the output is of the type SYM? If yes, give an example of one such string. If no, explain why not.
9.(6 pts) Suppose we wish to construct a code using input alphabet X = {0, 1}. 北美homework代写
(a) (1 pt) Give an example of a (3, 2) block code using input alphabet X.
(b) (1 pt) What is the rate of your code from (a)?
(c) (2 pt) Suppose you use your code from (a) on a channel with capacity 0.5. Is it possible that your code can achieve arbitrarily small probability of maximal block error? Explain why or why not.
(d) (2 pt) Suppose you use your code from (a) on a channel with unknown capacity. You fifind that the code can achieve arbitrarily small probability of maximal block error on this channel. What, if anything, can you conclude about the capacity of this channel?
10.(14 pts) Consider a channel over inputs X = {1, 2} and outputs Y = {1, 2} with transition matrix
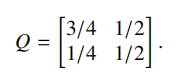
Let pX = (θ, 1 − θ) be a distribution over the inputs. Let H2(a) denote the entropy of a Bernoulli random variable with parameter a, i.e. H2(a) = −a · log a − (1− a) · log(1− a).
(a) (2 pt) Is Q symmetric? Explain why or why not.
(b) (3 pt) Compute p(Y = y) for y ∈ {1, 2}, expressing your answer in terms of θ.
(c) (2 pt) Compute H(Y |X), expressing your answer in terms of θ.
(d) (3 pt) Compute I(X;Y), expressing your answer in terms of θ.
(e) (3 pt) Show that the mutual information is maximised when θ satisfifies
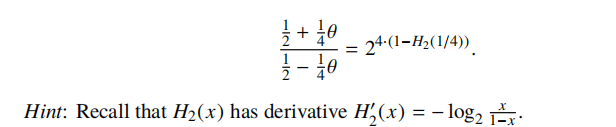
(f) (1 pt) How do the answers to parts (d) and (e) relate to the channel capacity of Q?
11.(3 pts) Calculate the value of the three parity bits for the message x = 1111 when it is coded using a (7, 4) Hamming code. You may use a diagram to show your working.
12.(2 pts) Two distinct notions of uncertainty we have looked at are (prefifix) Kolmogorov complexity K, and Shannon entropy H. What are the pros and cons of K versus H?




