DEPARTMENT OF MANAGEMENT SCIENCE
MSCI212: STATISTICAL METHODS FOR BUSINESS
Week 8 Workshop – An Introduction to Regression Modelling
回归建模代写 In the logging industry the value of a tree depends on the volume of wood in the tree trunk, as well as on the quality of the…
The Context
In the logging industry the value of a tree depends on the volume of wood in the tree trunk, as well as on the quality of the wood. The quality of wood is assessed by taking samples from a sample of trees to estimate the mean quality of each batch of logs. However the volume of wood in a tree trunk is difficult to measure, so that in practice a logging company needs to agree with its buyers a way of estimating the volume of wood from easy-to-obtain measurements.
The volumes of 31 trees (in cubic metres) have been carefully measured (using tanks of water) as well as their heights and diameters midway along the trunk (in feet) which are easy to measure. The data is stored in the SPSS file ‘MSCI212Trees.sav’.
Task 1: Basic Descriptive Statistics
Open the data file in SPSS and produce some basic descriptive statistics so you have a feel for the size of trees you are considering.
Task 2: Investigate the relationship (if any) between Volume and Height
Draw a scatterplot of Volume versus Height using
<Graphs><Legacy Dialogs><Scatterplot>:
Now ‘double-click’ on your scatterplot to give you the ‘Chart Editor’ dialogue box:
To add a ‘line of best fit’ click on the icon circled in red above, to get an extra dialog box:
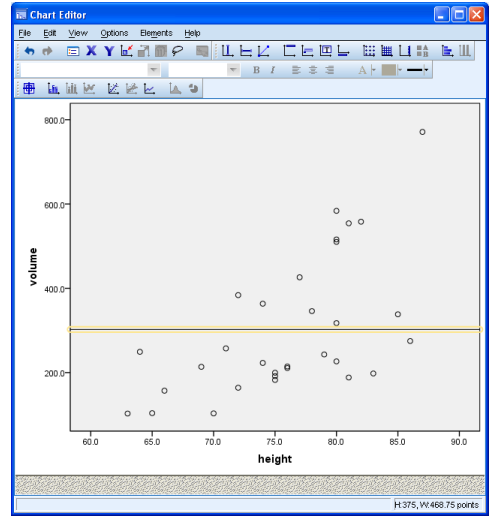
First of all click on [Mean of Y] and the click on [Apply], to show how the data varies about the average value of Y (you may need to drag the Properties dialogue box to one side to see the chart):
Now click on [Linear] and the click on [Apply] and the [Close] to show the ‘line of best fit’ through the data. You should then have:
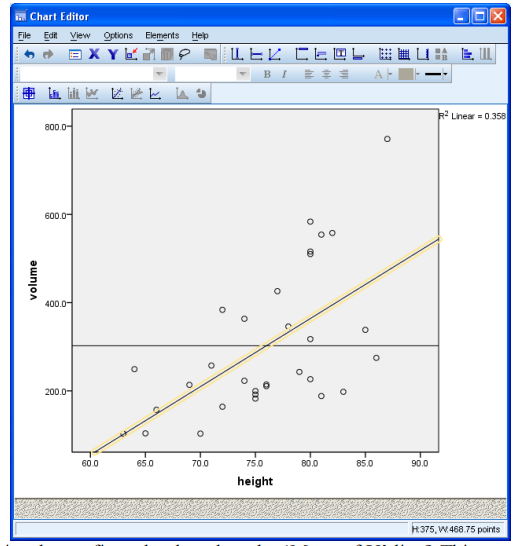
Do you agree that this is a better fit to the data than the ‘Mean of Y’ line? This suggests that there is some
sort of a relationship between the Volume and Height, although it is not a very good one.
Task 3: 回归建模代写
In order to obtain the equation of the line of best fit use:
<Analyze><Regression><Linear> and you get the dialogue box on the left below.
Select ‘volume’ as your Dependent Variable and ‘height’ as your Independent Variable, i.e.:
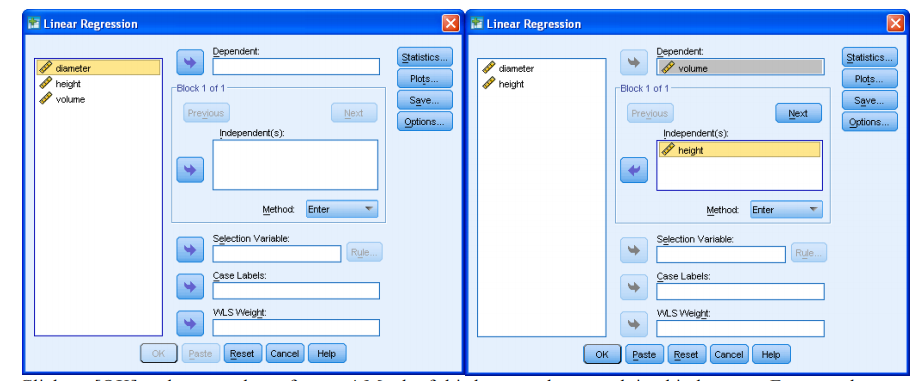
Click on [OK] and you get lots of output! Much of this has now been explained in lectures. For now there are just two items of interest to us, as circled below.
Regression 回归建模代写
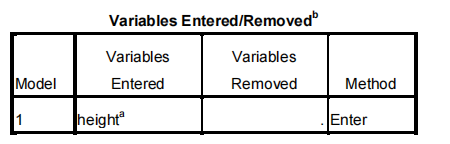
a.All requested variables entered.
b.Dependent Variable: volume
Model Summary
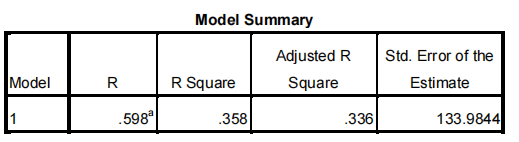
a.Predictors: (Constant), height
ANOVAb
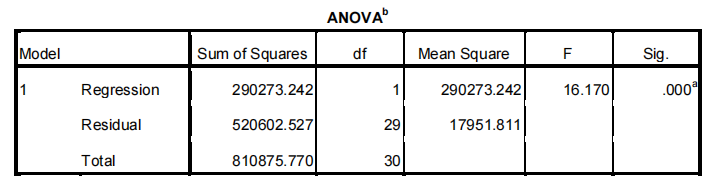
a.Predictors: (Constant), height
b.Dependent Variable: volume
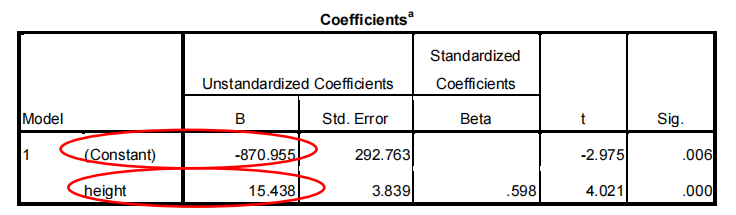
Coefficientsa
a.All requested variables entered.
b.Dependent Variable: volume
The equation of any fitted straight line model will be of the form:
Volume = A + B x Height +error
And the SPSS output is telling us that A = -870.955 and B = 15.438, i.e.
Volume = -871.0 + 15.4 x Height + error
a) What is the regression output telling us about whether or not the gradient is significantly different from zero?
b) And our earlier plots are warning us that the errors are pretty big! What is the estimated standard deviation of the errors (s)?
Task 4: Investigate the relationship (if any) between Volume and Diameter 回归建模代写
a) Following the method used in task 3, investigate the relationship between Volume and Diameter.
b) If you had to recommend that the logging company used one of your two relationships to estimate the Volume of wood in a tree which would you recommend, and why?
c) Use the equation of your recommended line of best fit to estimate the volume of a tree with height = 82ft and diameter = 15ft. How accurate do you think your estimate is?
Task 5: Can you find a better formula for predicting tree Volumes?
Can you think of a combination of height and diameter that might give a better estimate of tree volume?
For example if you thought that (height + diameter) might provide a good relationship you could try it out by first using <Transform><Compute variable> to create a new variable in your data sheet, called say ‘hplusd’as below:
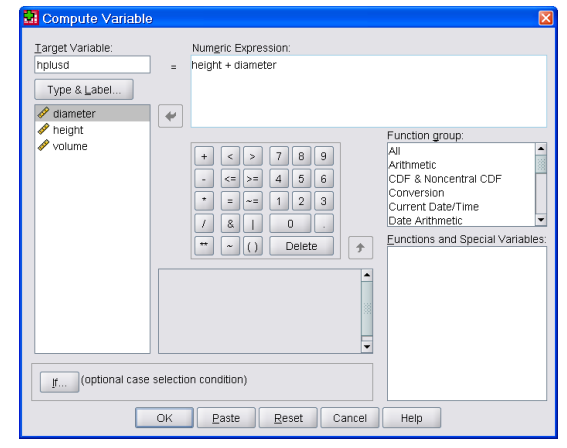
You can now investigate what relationship there is between Volume and ‘hplusd’ as in tasks 3 and 4.
- What is the best relationship that you can find? Use it to estimate the volume of a tree with height = 82ft and diameter = 15ft, and say how accurate you think it is.




