BEEM015 INDUSTRIAL ECONOMICS AND STRATEGY
MID-TERM EXAM
工业经济学与战略代考 Calculators are permitted. This is an open book exam. You will need to submit your answers via BART.
Calculators are permitted. This is an open book exam.
You will need to submit your answers via BART.
Your exam is an option 1 paper. This means it is an open-book non-invigilated exam. From the time that the exam paper is released, you will have 24 hours in which to complete and submit
your work.Please answer both questions. Both carry equal marks.
Please write in Ink/Ballpoint. 工业经济学与战略代考
- Consider a market for a homogeneous good, in which n=3 firms compete in quantities (Cournot model). The market demand function is given by p=24-Q, where p is the market price and Q the total quantity produced by all firms on the market. All firms can produce at constant marginal costs of c=4 per produced unit. There are no fixed costs.
(i) Find the Cournot-Nash equilibrium price and quantities.
(ii) Now suppose that two of the firms merge. Through the merger they are able to achieve efficiency gains, such that the marginal cost of production for the merged firm drops to c=2. Which of the three initial firms profit from this merger?
- Two firms (called F1 and F2) consider whether they should keep using their current technology or invest in a new technology that reduces CO2 emissions. Let the current technology be denoted by B (for Brown) and the new technology by G (for Green). Each firm independently and simultaneously chooses one of the two technologies, and their resulting profits (in millions of pounds) are shown in the normal form of the game below. In the matrix, F1 is the row player and F2 is the column player. The first number in a cell is F1’s profit and the second number is F2’s profit.
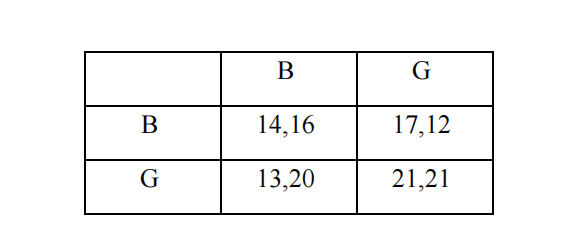
(i) Draw the best response curves of the two firms in one graph.
(ii) Find all Nash equilibria of the simultaneous game described above.
(iii) Now suppose the game is played sequentially, with F1 moving first. Draw the game tree and determine all subgame perfect Nash equilibria of this sequential game.



