Numerical Methods for Environmental Science
环境科学代写 Assessment of this project is via a scientifific report, describing what you have done and interpreting your fifindings in the…
Assessment of this project is via a scientifific report, describing what you have done and interpreting your fifindings in the context of the theory we have discussed in the past lectures. Write a report for this project, answering the questions in turn. Write in full sentences giving enough information so that a well-informed reader could understand your results without looking at the question sheet and your code. Re-phrase rather than copy questions. Include clear fifigures with correct legend and labels for both axis. Figures should be numbered and have captions. Your text answering the questions should refer to the figures by number. Submit your report and your code in the provided required format. The hand out date is 3 rd June 2021 23:59. Submit the word-processed report along with final version of your program (single python file) on chaman@nuist.edu.cn or my WeChat.
In this assessment report you will be analysing and writing code to solve the oscillation equation, given below: 环境科学代写
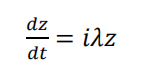
where z = x + ?y is the complex valued, time dependent unknown, t is time, ?= √ −1 and λ is a real valued constant.![]() is the rate of change of z (complex value) with respect to time.
is the rate of change of z (complex value) with respect to time.
This equation could represent the location of a parcel of air in a cyclone (Figure 1). Remember the position of the projection of air parcel in cyclone performs simple harmonic motion, and the expression is the same one we are observing for the position of a simple harmonic oscillator in simple harmonic motion. Four numerical methods for solving (1) are given below in equations 2 to 5.These equations use a time step ∆t and assume that ?? is ? at time n∆t for time step number “n”. 环境科学代写
Euler Explicit ??+1 = (1 + ????)?? (2)
Euler Implicit ??+1 = ?? + ??????+1 (3)
Crank-Nicolson 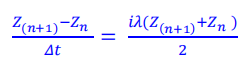 (4)
(4)
Leapfrog ??+1 − ??−1 = 2?????? (5)
Above numerical methods are for solving the oscillation equation (1). Order of accuracy for Euler methods is one and for Crank-Nicolson and Leapfrog is two. Amplification factor, A for Euler explicit and implicit method is 1 + ???? and (1 + ????)/(1 + ?²??²) respectively.
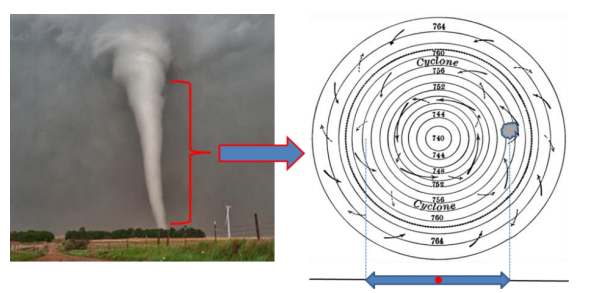
Figure1: Cyclone air, position of the projection of air parcel in cyclone performs simple harmonic motion.
- When the amplification factor “A” is complex, the scheme is stable when the magnitude of the amplification factor is less than one. (Remember that for a complex number, z = x + ?y, ||z|| = √x2 + y2 .) Find the square of the magnitude of the amplification factor for each of the schemes present in equations 2 to 5 and deduce which schemes are stable and which are damping. In case of Crank-Nicolson and Leapfrog methods, first you need to find the amplification factor “A” for solving the oscillation equation and Then Square of the magnitude of the amplification factor. Make sure that the denominator of any complex number is real by multiplying top and bottom by the complex conjugate. (Remember that for a complex number, z = x + ?y, z∗ = x – ?y )[10 marks].
————————————————————————–
- The provided code in separate files solves the oscillation equation using Euler explicit and Euler implicit and plots the results. Add functions to solve the equation using the Crank-Nicolson and Leapfrog methods. Solve the oscillation equation using the first set of parameter values given in table below. Plot the real part of the solutions against time from all four schemes on the same graph. On a separate graph, plot the errors as a function of time. Describe and explain the results. Parameter values for solving the oscillation equation are given below. N is the total number of time steps [10 marks].
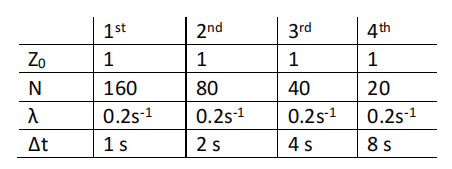
-
Run the code with the fourth parameter set from above table in question 2. Plot, present and explain the results [10 marks]. 环境科学代写
- Run the code with each parameter set but adjust N so that the total run time is just 16 seconds for each simulation. Calculate the error at the final time for each simulation. Plot the absolute value of the error as a function of time step. Describe and explain the results [10 marks].
————————————————————————–
- The last question of the report is related to simulation of a simple pendulum on python language. A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position. The mathematical model for a simple pendulum is given by differential equation
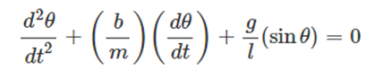
Split the given second-order differential equation (6) in to two first-order differential equations. You need to write the time-stepping code to solve the two first-order differential equations. Run the code with parameter set given in table 1. [4 marks].

Table 1: Initial values for solving the equation (6), 环境科学代写
Plot the below parameters on single combined graph [6 marks].
a. Angular displacement vs time graph (set the line colour black)
b. Angular velocity vs time graph (set the line colour blue)
c. Angular acceleration vs time graph (set the line colour red)
The plots should have x and y labels, legend and caption.
==============END of the assessment=================



