project1
算法代码代写 We had lots of fun with the 8-Queens problem. In this project you will implement several search and constraint optimization algorithms for…
1 Project 1
1.1 Requirement: 算法代码代写
We had lots of fun with the 8-Queens problem. In this project you will implement several search and constraint optimization algorithms for generating solutions to the 8-Queens problem. Implement four of your favorite algorithms for solving the 8-Queens problem using any language you like. Diversity in chosen search algorithms is expected. Compare their performance using appropriate metrics.
1.2 Summary
In this project, we should use 4 different algorithms to solve the 8_Queens problem, and compare those 4 algorithm. I decided to use Simulates Annealing, Back Tracking, BFS and DFS to find only one solution of 8-Queens. First, I write the 4 algorithms code, then I only print one solution, and record their running time for comparison. I put the running time in metric, and I also draw a bar graph to visualize the running time data.
[1]: import random from math import exp import time from copy import deepcopy import numpy as np import pandas as pd import seaborn as sns from matplotlib.pyplot import figure
2 Simulated Annealing 算法代码代写
[115]: N_QUEENS = 8
TEMPERATURE = 400
def threat_calculator(n):
if n < 2:
return 0
elif n == 2:
return 1
return (n - 1) * n / 2
def create_board(n):
chess_board = {}
temp = list(range(n))
random.shuffle(temp)
column = 0
while len(temp) > 0:
row = random.choice(temp)
chess_board[column] = row
temp.remove(row)
column += 1
del temp
return chess_board
def cost(chess_board):
threat = 0
m_chessboard = {}
a_chessboard = {}
for column in chess_board:
temp_m = column - chess_board[column]
temp_a = column + chess_board[column]
m_chessboard[temp_m] = 1 if (temp_m not in m_chessboard) else ␣
, →m_chessboard[temp_m]+1
a_chessboard[temp_a] = 1 if (temp_a not in a_chessboard) else ␣
, →a_chessboard[temp_a]+ 1
for i in m_chessboard:
threat += threat_calculator(m_chessboard[i])
del m_chessboard
for i in a_chessboard:
threat += threat_calculator(a_chessboard[i])
del a_chessboard
return threat
def simulated_annealing():
2solution_found = False
answer = create_board(N_QUEENS)
cost_answer = cost(answer)
t = TEMPERATURE
sch = 0.99
while t > 0:
t *= sch
successor = deepcopy(answer)
while True:
index_1 = random.randrange(0, N_QUEENS - 1)
index_2 = random.randrange(0, N_QUEENS - 1)
if index_1 != index_2:
break
successor[index_1], successor[index_2] = successor[index_2], \
successor[index_1]
# swap two chosen queens
delta = cost(successor) - cost_answer
if delta < 0 or random.uniform(0, 1) < exp(-delta / t):
answer = deepcopy(successor)
cost_answer = cost(answer)
if cost_answer == 0:
solution_found = True
print_chess_board(answer)
break
def print_chess_board(board):
print('Simulated Annealing:')
b = [ [0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
]
for column, row in board.items():
b[row][column]=1
3for i in range(N):
for j in range(N):
print (b[i][j],end=' ')
print()
tic = time.perf_counter()
simulated_annealing()
toc = time.perf_counter()
print("Runtime in second:", toc-tic)
Simulated Annealing:
0 0 1 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 1 0 0 0 0 0 0
0 0 0 0 0 1 0 0
Runtime in second: 0.00736125500043272
Simulated Annealing is a algorithm. It is the probabilistic wau to find the global maximun in function. when it has higher temperature, it can search larger range of the function.
3 Back_Tracking 算法代码代写
[122]: global N
N = 8
def create_board(board):
for i in range(N):
for j in range(N):
print (board[i][j],end=' ')
print()
def check(board, row, col):
i=0
while i <col:
if board[row][i] == 1:
return False
i=i+1
for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
if board[i][j] == 1:
return False
for i, j in zip(range(row, N, 1), range(col, -1, -1)):
if board[i][j] == 1:
return False
return True
def back_tracking(board, col):
if col >= N:
return True
else:
i=0
while i < N:
if check(board, i, col):
board[i][col] = 1
if back_tracking(board, col + 1) == True:
return True
board[i][col] = 0
i=i+1
return False
def print_chess_board():
print('Back_Tracking:')
board = [ [0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
5[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0],
]
if back_tracking(board, 0) == False:
return False
create_board(board)
return True
tic = time.perf_counter()
print_chess_board()
toc = time.perf_counter()
print("Runtime in second:", toc-tic)
Back_Tracking:
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
Runtime in second: 0.0023467620012525003 算法代码代写
Back Tracking is a general algorithm to find solution. It try as many way as it can, when it do calculation. But, when Back Tracking find some way it tried can not solve the problem, it will give up the ways and cancel the previous calculation of the ways. It’s time complexity is O(N!).
4 BFS
[143]: def check(seqs, pos):
a = np.array([0] * 81)
a = a.reshape(9, 9)
n = 0
i=0
while i<=pos:
a[seqs[i – 1]][i] = 1
i=i+1
6i=0
while i <=pos:
for k in list(range(1, i)) + list(range(i + 1, 9)):
if a[seqs[i – 1]][k] == 1:
n += 1
t1 = t2 = seqs[i – 1]
for j in range(i – 1, 0, -1):
if t1 != 1:
t1 -= 1
if a[t1][j] == 1:
n += 1
#
elif t2 != 8:
t2 += 1
if a[t2][j] == 1:
n += 1
t1 = t2 = seqs[i – 1]
for j in range(i + 1, 9):
if t1 != 1:
t1 -= 1
if a[t1][j] == 1:
n += 1
#
elif t2 != 8:
t2 += 1
if a[t2][j] == 1:
n += 1
i=i+1
return int(n/2)
def print_chess_board(seqs):
board = np.array([0] * 81)
board = board.reshape(9, 9)
for i in range(1, 9):
board[seqs[i – 1]][i] = 1
print(‘BFS:’)
for i in board[1:]:
for j in i[1:]:
print(j, ”, end=””)
print()
7tic = time.perf_counter()
frontier_queue = [[0] * 8]
solution = []
flag = 0
while frontier_queue:
if flag == 1:
break
seqs = frontier_queue.pop(0)
nums = list(range(1, 9))
for j in range(8):
pos = seqs.index(0)
temp_seqs = list(seqs)
temp = random.choice(nums)
temp_seqs[pos] = temp
nums.remove(temp)
if check(temp_seqs,pos) == 0:
frontier_queue.append(temp_seqs)
if 0 not in temp_seqs:
solution = temp_seqs
flag = 1
break
print_chess_board(solution)
toc = time.perf_counter()
print(“Runtime in second:”, toc-tic)
BFS:
1 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0
0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 0 1 0 0 0
Runtime in second: 0.7307305437998366
BFS is an algorithm for searching. For example, when we use it to search a tree. It searches the tree leval by leval, and then get the solution. The time complexity is O(V+E)
5 DFS 算法代码代写
[141]: def check(seqs, pos):
a = np.array([0] * 81)
a = a.reshape(9, 9)
n = 0
i=0
while i<=pos:
a[seqs[i - 1]][i] = 1
i=i+1
i=0
while i <=pos:
for k in list(range(1, i)) + list(range(i + 1, 9)):
if a[seqs[i - 1]][k] == 1:
n += 1
t1 = t2 = seqs[i - 1]
for j in range(i - 1, 0, -1):
if t1 != 1:
t1 -= 1
if a[t1][j] == 1:
n += 1
#
elif t2 != 8:
t2 += 1
if a[t2][j] == 1:
n += 1
t1 = t2 = seqs[i - 1]
for j in range(i + 1, 9):
if t1 != 1:
t1 -= 1
if a[t1][j] == 1:
n += 1
#
elif t2 != 8:
t2 += 1
if a[t2][j] == 1:
n += 1
i=i+1
return int(n/2)
9def print_chess_board(seqs):
board = np.array([0] * 81)
board = board.reshape(9, 9)
for i in range(1, 9):
board[seqs[i - 1]][i] = 1
print('DFS:')
for i in board[1:]:
for j in i[1:]:
print(j, '', end="")
print()
tic = time.perf_counter()
start = time.time()
frontier_stack = [[0] * 8]
solution = []
flag = 0
while frontier_stack:
if flag == 1:
break
seqs = frontier_stack.pop(-1)
nums = list(range(1, 9))
for j in range(8):
pos = seqs.index(0)
temp_seqs = list(seqs)
temp = random.choice(nums)
temp_seqs[pos] = temp
nums.remove(temp)
if check(temp_seqs,pos) == 0:
frontier_stack.append(temp_seqs)
if 0 not in temp_seqs:
solution = temp_seqs
flag = 1
break
print_chess_board(solution)
toc = time.perf_counter()
10print("Runtime in second:", toc-tic)
DFS:
0 0 0 0 1 0 0 0
0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 0 1 0
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
1 0 0 0 0 0 0 0
Runtime in second: 0.2118144010019023
DFS is an algoritnm used for searching. For example when we use it to search a tree, it gose as long as possible. It is not like the BFS. It does not search tree leval by leval. the time complexity of DFS is O(V+E). 算法代码代写
6 Comparison of 4 Algorithm
[2]: df = pd.DataFrame() df['Algorithm'] = ['Simulated Annealing', 'Back Tracking', 'BFS','DFS'] df['Running time'] = [0.00736125500043272, 0.0023467620012525003, 0. , →7307305437998366,0.2118144010019023] df [2]: Algorithm Running time 0 Simulated Annealing 0.007361 1 Back Tracking 0.002347 2 BFS 0.730731 3 DFS 0.211814 [21]: sns.set(font_scale =2) figure(figsize=(15,10 )) sns.barplot(data=df, x="Algorithm",y='Running time') [21]: <matplotlib.axes._subplots.AxesSubplot at 0x1a2893b750>
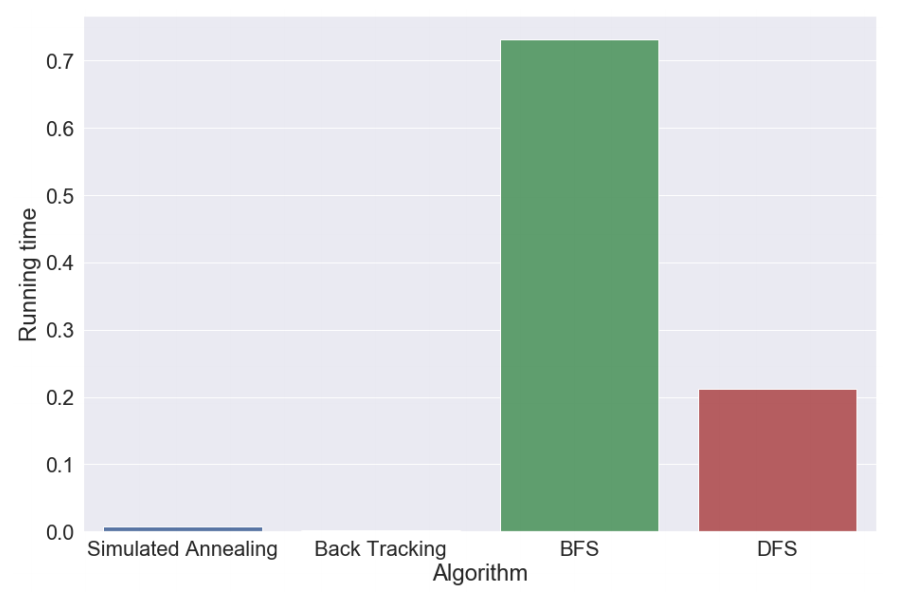
According to the metrics. We find that Back Tracking using the shortest time. BFS uses the longest time. For simple N-Queens problem, for example 8-Queens, we can use Back Tracking. It can gives us solution during short time. But, If we want to solve more complex N-Queens problem, we should use a better algorithm, like Simulates Annealing. When we increase the temperature of Simulates Annealing, we can search larger range. Thus, we can get more solutions.




