财务作业代写
财务作业代写 本文遵循以下假设条件构建函数模型:
(1)船舶航行成本仅考虑燃油成本;
(2)不考虑船舶航行过程中在节点的停靠时间;
(3)海盗船舶航行方向和速度保持不变;
(4)目标船舶航行速度保持不变;
(5)最优路径 L 包含边的上限为 A;
(6)最优路径 L 花费时间的上限为 T。
基本假设
本文遵循以下假设条件构建函数模型:
(1)船舶航行成本仅考虑燃油成本;
(2)不考虑船舶航行过程中在节点的停靠时间;
(3)海盗船舶航行方向和速度保持不变;
(4)目标船舶航行速度保持不变;
(5)最优路径 L 包含边的上限为 A;
(6)最优路径 L 花费时间的上限为 T。
变量定义 财务作业代写
L- s 到 d 可行路径的所有集合;
T l s d – s 到 d 可行路径 l 上总花费航行时间;
C1( l s d )– s 到 d 可行路径 l上燃油总成本;
C2( l s d )— s 到 d 可行路径 l 上海盗袭击风险总成本;


目标函数
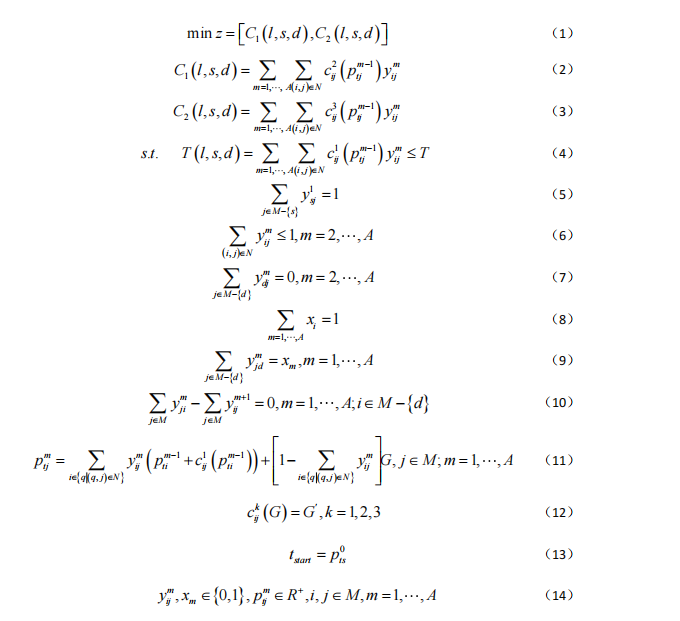
目标函数(1)表示燃油成本最小和海盗袭击风险成本最小的目标函数;公式(2)表示路径 l 上的燃油成本;公式(3)表示路径 l上
的海盗袭击风险成本;约束(4)表示船舶在路径 l 上航行总时间小于等于 T;约束(5)表示从 s 指向 j 的第一条有向边是路径 l 上的;约束(6)表示在 i 和 j 之间有且仅有 1 次机会成为路径 l 上的第 m 条边;约束(7)表示在路径 l上 d 是终点;约束(8)表示在路径 l 上边的数量;约束(9)表示路径 l 将在终点 d 处结束;约束(10)表示流量守恒,保证在路径 l 上的流入边和流出边是连续的且每个节点仅有 1 条流入边和 1 条流出边;约束(11)表示到达 j 的时间,其中 G 为无穷大;约束(12)中G 也为无穷大,表示当到达 j 的时间为 G 时,从点i 到点 j 的航行时间、燃油成本、海盗袭击风险成本都为 G;约束(13)表示从 s 出发的起始时间;约束(14)表示变量约束条件。
对环境进行栅格化处理
这篇文章对研究海域环境进行栅格化处理,按一定的比例将研究区域划分为栅格图,且栅格图中各个节点之间的有向边可存储数据。如图 1 所示在 4×4 的栅格中,每个节点可以连接 16 个相邻不同方向的节点,节点需满足以下条件:
(1)节点和节点间的有向边都位于海上;
(2)节点处和节点间的有向边处都需具有足够水深。
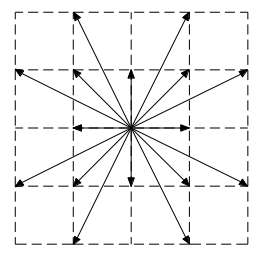
图 1 相邻节点图
燃油成本 财务作业代写
本文将燃油成本定义为在路径 l 上的总燃油消耗量,总燃油成本为总航行时间乘以单位时间的油耗。
C1 (l,s,d)=T (l,s,d) · E · f (15)
式中 E 为单位时间油耗;f 为燃油价格。其中单位时间油耗由船舶额定功率和额定功率下油耗决定,如公式(16)所示:
E =r · W (16)
式中 r 为额定功率下燃油消耗率;W 为船舶额定功率。
海盗袭击风险成本
本文将海盗袭击风险成本定义为海盗袭击的概率与袭击造成财
产损失的乘积。
C2 (l,s,d)=s+w · d (17)
式中 s 为海盗袭击平均成本;w 为海盗袭击概率;d 为海盗袭击所造成的财产损失。



