Mock Exam
金融数学代考 This exam has 4 questions, plus an additional fifinal question for M4/M5 students. [default,O3f]Consider the following one…
This exam has 4 questions, plus an additional fifinal question for M4/M5 students.
Question 1 金融数学代考
(Total: 20 marks)
[default,O3f]Consider the following one period trinomial model: Ω = {ω1, ω2, ω3}, P(ωi) = 1/3 for i = 1, 2, 3, a bank account B with interest rate r = 0, and one stock S with S0 = 10 and
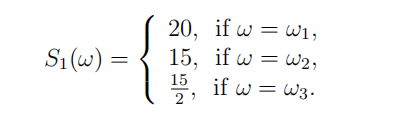
Consider a forward contract on the stock, which has payoffff F1(K) := S1 −K at time 1 and cost F0(K) := 0 at time 0; and a derivative with time 1 payoffff X1(ωi) := xi , i = 1, 2, 3 and time 0 cost X0. Answer the following questions and justify carefully with either proofs or counterexamples.
(a) (2 points) What is a replicating strategy for the forward contract?
(b) (3 points) Fix K = 8. Explicitly build an arbitrage in the market (B, S, F(K)).
(c) (4 points) For what value(s) of K is the market (B, S, F(K)) is arbitrage free?
From now on, fifix one such value K∗ of K.
(d) (2 points) Is the (B, S, F(K∗ )) market complete?
(e) (4 points) If X0 = 0, for which values of x = (xi)i=1,2,3 ∈ R3 , is the derivative X replicable in the (B, S, F(K∗ )) market? Does the answer change if X0 = 5?
(f) (5 points) If the market consists of (B, S, F(K∗ )) and x = (10, 6, 0), are there values of X0 for which you would be willing to sell the derivative X irrespectively of your attitude towards risk? If so, which one(s)? What if instead x = (10, 6, 4) ?
Question 2 金融数学代考
(Total: 20 marks)
[default,M5b]
In the framework of the N-period binomial model with constant parameters S0 = 8, u = 2, d = 1/2, r = 0, let S = (Sn)Nn=0 be the stock price process, and Ln (resp. Mn) its historical minimum (resp. maximum) up to time n (i.e. Ln := mini=0,…,n Si , Mn := maxi=0,…,n Si).
Consider the option which, at maturity N, pays MN −LN if the stock price has never risen above 15 and never fallen below 3; the option pays 0 otherwise. We denote with Vn the arbitrage-free price at time n = 0, . . . , N of this option.
Below, whenever we say that a process is Markov, we mean with respect to the risk-neutral measure Q and with the usual fifiltration Fn = σ(X1, . . . , Xn), n = 0, . . . , N generated by the coin tosses Xn(ω) = ωn on the probability space Ω = {H, T}N . Answer the following questions and justify carefully with either proofs or counterexamples.
(a) (2 points) Use the risk-neutral pricing formula to express Vn in terms of Vn+1.
(b) (3 points) Is M a Markov process?
(c) (4 points) Prove that A := (L, M) is not a Markov process
(d) (4 points) Prove that B := (S, L, M) is a Markov process.
(e) (7 points) Work by backward induction to show that, for every n = 0, . . . , N, Vn admits the representation Vn = hn(Bn) for some (deterministic) function hn. Write explicitly hN and an explicit formula to express hn in terms of hn+1 for n = 0, . . . , N − 1.
Question 3 金融数学代考
(Total: 20 marks)
[default,M15]
Consider a market (Bn, Sn)n=0,1,…,T described by a multi-period binomial model with constant parameters 0 < d < 1 + r < u, and as usual let Fk = σ(X1, . . . , Xk), 0 ≤ k ≤ T be the fifiltration generated by the coin tosses (Xi)i . Consider a forward-start call option, which entitles its holder to receive at time T0 ∈ N, T0 < T a call option (on the stock S) with maturity T and strike KST0 (where K > 0). Answer the following questions, and (other than in item (a)) justify carefully with proofs.
(a) (5 points) Write down a formula, involving the expectation with respect to the risk-neutral measure Q, for
V0 := the price at time 0 of the forward-start call option.
(b) Show that, if {Xi}i∈I are independent random vectors and {fi}i∈I are Borel functions then {fi(Xi)}i∈I are independent random vectors
(c) (4 points) Prove that the random variables

(f) (6 points) Show that V0 = c(T − T0, Kx), where c(t, x) is the price at time 0 of a call option with expiry t and S0 = x.
Question 4
(Total: 25 marks)
[default,C4]
In this exercise consider the Black and Scholes market model (Bt , St)t , and some derivatives, all of which have the same underlying S. Denote with Ft(T)/Ct(T, K)/Pt(T, K) the value (i.e. the arbitrage-free price) at time t ∈ [0, T] of a forward contract/a call option with strike K/a put option with strike K (all with expiry T).
(a) (2 points) Replicate the forward contract with a static portfolio made of the underlying S and the bank account B, i.e. determine constants a, b ∈ R such that
Ft(T) = aSt + bBt a.s. for all t ∈ [0, T].
(b) (3 points) Replicate the forward contract with a static portfolio made of calls and puts, by determining constants
c, d ∈ R s.t. Ft(T) = cCt(T, K) + dPt(T, K) a.s. for all t ∈ [0, T],
where K := ST − FT (T) ∈ R is the forward price of the underlying.
(c) (3 points) Denote with c = c(τ, x, K) the function (which we computed in class) such that 金融数学代考
c(T − t, St , K) = Ct(T, K)
is the price at time t of the call option with expiry T and strike K in the Black and Scholes model. Write a formula, involving the value of St of the underlying and the function c, for the price Pt(T, K) of the put option in the Black and Scholes model.
(d) (7 points) Fix a date t ∈ (0, T) and consider a chooser option with parameter t, i.e. the contract which gives its owner the right to choose, at time t, whether to receive either a call or a put option (both with expiry T and strike K). Denote with Vs its value at time s ∈ [0, T]. Defifine functions f = f(x, y), g = g(x, y) such that the values Vt , VT of the chooser option are given by
Vt = f(Ct , Pt), VT = g(St , ST ) a.s..
(e) (4 points) Show that
Vt = Ct + (Ke−r(T −t) − St)+
(f) (6 points) Use (3) to show that the initial price (i.e. the value at time 0) V0 of the chooser option is the sum of the initial prices of some call and of put options, by determining strike prices KC, KP ≥ 0, expiries TC, TP ∈ [0, T], and constants e, f ∈ R such that
V0 = eC0(TC, KC) + fP0(TP , KP ).
Question 5 金融数学代考
(Total: 20 marks)
[default,O20b]On the sample space Ω = {ωi}i=1,…,3 endowed with some probability P s.t. P(ωi) > 0 for all i, consider a one-period arbitrage-free market model with a bank account, and a stock S with prices S0 = 3, S1 =(3,6,12)T. Assume for now, as we usually do, that the interest rate r for lending and for borrowing is the same. For a derivative with payoffff X1, we consider the problem (P) of fifinding the smallest initial capital p of a portfolio super-replicating X1 P a.s.. If we express the portfolio as a function of the number h ∈ R of shares and of the amount of cash c ∈ R in the bank account (instead of the initial capital x), then (P) is the following LP (Linear Program):
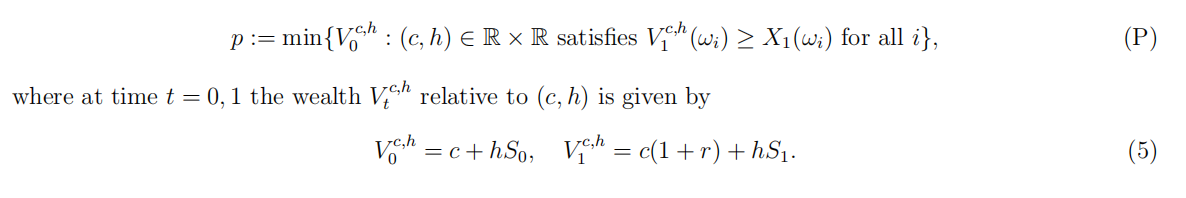
Assume from now on that the bank offffers an interest rate rd ≥ 0 on deposits, whereas one can borrow money from the bank at the interest rate rb ≥ rd. Answer the following questions and justify carefully with either proofs or counterexamples.
(a) (3 points) Write a formula for the value of a portfolio V1 m,h at times t = 0, 1 as a function of the following variables: md, mb ∈ R+, h ∈ R, where md (resp. mb) represents the amount of money the investor deposited in (resp. borrowed from) the bank at time 0, m = (md, mb), and h ∈ R represents the number of shares bought1 at time 0.
(b) (1 point) Suppose for this item that rd = rb = r. Are V1 m,h and V1 c,h equal when md = c+, mb = c−? Are they equal when md = 1 + c+, mb = 1 + c−? 金融数学代考
(c) (3 points) Suppose from now on that rd = 1, rb = 2. Call (P*) the LP of fifinding the smallest initial capital p∗ of a portfolio super-replicating a derivative with payoffff X1 P a.s., i.e. (P*) is what you obtain from (P) replacing with Vt c,h with Vt m,h. To avoid dealing with a non-linear constraint, when defifining the super-replication problem (P*), we did not impose that mdmb = 0.
(6) Does any optimal solution of (P*) automatically satisfy (6)? Would the infifimum defifining (P*) have been strictly bigger if we had imposed the additional constraint (6)?
(d) (2 points) Is p∗ is bigger (meaning ≥) than the value of p (defifined in (P)) corresponding to r = 1, for any choice of X1? Is it always strictly bigger?
(e) (5 points) Use formulas to defifine what is an arbitrage in this market, and then answer: does this market admit an arbitrage?
(f) (6 points) Consider a derivative with payoffff X1 :=(2,3,4)T. Solve (P*), i.e. fifind its optimiser(s), and its optimal value p∗.




